Kraft

Die Kraft gibt an, wie stark zwei Körper aufeinander einwirken. Die Kraft ist eine Wechselwirkungsgröße und eine gerichtete (vektorielle) Größe. Die Wirkung einer Kraft ist abhängig von ihrem Betrag, von ihrer Richtung und von ihrem Angriffspunkt.

Formelzeichen:	$\vec{F}$
Einheit:	ein Newton (1 N)

Man unterscheidet u. a. elektrische Kräfte, magnetische Kräfte, Reibungskräfte, Gewichtskräfte, Adhäsionskräfte und Kohäsionskräfte voneinander.

Die Kraft gibt an, wie stark zwei Körper aufeinander einwirken.

Formelzeichen:	$\vec{F}$
Einheit:	ein Newton (1 N)

Ein Newton (1 N) ist die Kraft, die einem Körper der Masse 1 kg eine Beschleunigung von $1 \frac{m}{s^{2}}$ erteilt. Es ist etwa die Kraft, mit der ein Körper der Masse 100 g auf eine ruhende Unterlage drückt oder an einer Aufhängung zieht (Bild 2). Benannt ist diese Einheit nach dem berühmten englischen Physiker ISAAC NEWTON (1643-1727).

Vielfache der Einheit 1 N sind ein Kilonewton
(1 kN) und ein Meganewton (1 MN):

1 kN = 1 000 N
1 MN = 1 000 000 N

Die Einheit 1 N

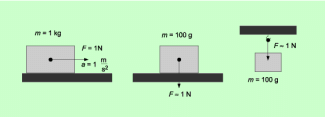
Charakterisierung der physikalischen Größe Kraft

Die Kraft ist eine Wechselwirkungsgröße. Sie wirkt immer zwischen zwei oder mehreren Körpern, wobei die Körper wechselseitig aufeinander einwirken. Dabei gilt das Wechselwirkungsgesetz, das besagt: Wirken zwei Körper wechselseitig aufeinander ein, so sind die Kräfte gleich groß und entgegengesetzt gerichtet.
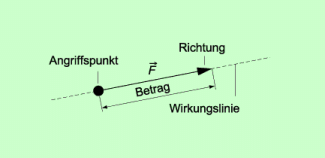
Die Kraft ist eine gerichtete (vektorielle) Größe. Sie wird mithilfe von Pfeilen dargestellt. Jede Kraft hat eine Richtung, einen Betrag und einen Angriffspunkt (Bild 3). Der Buchstabe F ohne Pfeil bedeutet immer den Betrag der Kraft.
Kräfte sind nur an ihren Wirkungen erkennbar. Die Wirkung einer Kraft ist abhängig

vom Betrag der Kraft,
von der Richtung der Kraft,
vom Angriffspunkt der Kraft.

Kraft als gerichtete Größe

Kräfte können Bewegungsänderungen von Körpern, Formänderungen von Körpern (elastische oder plastische Verformung) oder deren Zerstörung hervorrufen.

In der nachfolgenden Übersicht sind die Beträge von Kräften aus Natur und Technik angegeben.

Kräfte in Natur und Technik

Gewichtskräfte ein 10-Cent-Stück 1 Tafel Schokolade 1 Liter Wasser Mensch PKW	0,04 N 1 N 10 N 500 N ... 800 N etwa 10 000 N
Zugkräfte und Schubkräfte Pferd PKW Lokomotive	400 N ... 750 N 5 000 N 200 000 N
Hubkräfte Gewichtheben Eisenbahndrehkran	1 000 N ... 2 500 N bis 2 500 000 N
Auftriebskräfte Ball (d = 30 cm) Schiff (Wasserverdrängung 20)	139 N 196 000 N
Luftwiderstandskraft PKW bei 100 km/h	etwa 210 N

Messen von Kräften

Kräfte können mithilfe unterschiedlicher Messverfahren bestimmt werden. Unterschieden wird zwischen der statischen und der dynamischen Kraftmessung.

Statische Kraftmessung: Man misst Kräfte mithilfe von Federkraftmessern. Die Kraft kann direkt an der Skala des Federkraftmessers abgelesen werden. Nähere Erläuterungen sind unter dem Thema "Federkraftmesser" zu finden.

Dynamische Kraftmessung: Es wird der Zusammenhang zwischen der Kraft, der Beschleunigung und der Masse eines Körpers (newtonsches Grundgesetz) genutzt. Kennt man die Masse m eines Körpers und seine Beschleunigung a, so ergibt sich der Betrag der beschleunigenden Kraft nach der Gleichung $F = m \cdot a$ .

Berechnen von Kräften

Allgemein kann die Kraft mit der Gleichung $F = m \cdot a$ berechnet werden. Für spezielle Kräfte sind auch spezielle Gleichungen anzuwenden. Nachfolgend sind die wichtigsten Kräfte mit ihren Berechnungsmöglichkeiten genannt.

Art der Kraft	Berechnungs- möglichkeit	Bedeutung der Größen
allgemein	$F = m \cdot a$	m Masse des Körpers a Beschleunigung des Körpers
Gewichtskraft	$F_{G} = m \cdot g$	m Masse des Körpers g Fallbeschleunigung (Ortsfaktor)
Reibungskraft	$F_{R} = μ \cdot F_{N}$	$\begin{array}{l} μ Reibungszahl \\ F_{N} Normalkraft \end{array}$
Federspannkraft	$F_{S} = D \cdot s$	D Federkonstante s Längenänderung der Feder
Radialkraft (Zentralkraft)	$F_{r} = m \cdot \frac{v^{2}}{r} = m \cdot \frac{4 π^{2} \cdot r}{T^{2}}$	m Masse des Körpers v Geschwindigkeit des Körpers r Radius der Kreisbahn
Auftriebskraft	$F_{A} = ρ \cdot V \cdot g$	$\begin{array}{l} ρ Dichte \\ V Volumen \\ g Fallbeschleunigung \\ (Ortsfaktor) \end{array}$
Gravitationskraft	$F = G \cdot \frac{m_{1} \cdot m_{2}}{r^{2}}$	$\begin{array}{l} G Gravitationskonstante \\ m_{1}, m_{2} Massen der Körper \\ r Abstand der \\ Massemittelpunkte \end{array}$

Arten von Kräften

Es gibt viele verschiedene Arten von Kräften, die man z. B. nach der Art ihrer Entstehung oder nach der Art ihres Wirkens einteilen kann. Einige dieser Kräfte sind in der Tabelle oben genannt. Nach der Art ihres physikalischen Charakters kann man weitere Kräfte unterscheiden. Nachfolgend ist dazu eine Übersicht gegeben.

Wirkungen von Kräften

Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.

Physik Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Physik kostenlos lernen

Verwandte Artikel

Kraft

Charakterisierung der physikalischen Größe Kraft

Messen von Kräften

Berechnen von Kräften

Arten von Kräften

Rechtliches

Einloggen