Johannes Kepler
Leben und Wirken
JOHANNES KEPLER wurde am 27. Dezember 1571 in Weil, einer kleinen Stadt in Württemberg, geboren. Sein Vater kümmerte sich kaum um ihn, da er in jener unruhigen Zeit jahrelang mit Landsknechtsheeren unterwegs war.
Bekannt aus KEPLERs Kindheit und Jugendzeit ist nur, dass er als armer Stipendiat das Gymnasium in Maulbronn besuchte und anschließend an der württembergischen Landesuniversität in Tübingen studierte. Hier beschäftigte er sich mit lutherischer Theologie, Mathematik und Astronomie.
Insbesondere lernte KEPLER die Ideen des NIKOLAUS KOPERNIKUS (1473 bis 1543) kennen und wurde schnell zu einem Anhänger von dessen Lehre. Diese war damals keineswegs allgemein anerkannt und wurde besonders von der Kirche scharf angegriffen, weil sie den Dogmen von der Zentralstellung der Erde widersprach.
Noch vor Abschluss seiner theologischen Studien wurde KEPLER nach Graz geschickt, um dort als protestantische Lehrkraft zu wirken. So wurde er 1594 „Lehrer der Mathematik und Moral“ am Gymnasium in Graz und zugleich Mathematiker der neuen protestantischen Landesregierung.
Damit hatte er die Pflicht, jährlich einen amtlichen Kalender auszuarbeiten, der auch astronomische Angaben über Sonne, Mond, Planeten und den Tierkreis, den voraussichtlichen Witterungsablauf und zu erwartende besondere Ereignisse enthielt. Diese Aufgabe, die auch astronomische Berechnungen erforderte, hat KEPLER – nach eigenen Aussagen – endgültig zur Astronomie und Mathematik hingeführt.
1599 wurde die Steiermark wieder katholisch und KEPLER musste sich nach einer neuen Beschäftigung umsehen. Er fand sie in Prag bei dem berühmten dänischen Astronomen TYCHO BRAHE (1546 bis 1601), dessen Mitarbeiter er wurde. Nach dem Tod BRAHEs war KEPLER als Hofastronom des deutschen Kaisers RUDOLF II. (1552 bis 1612) in Prag tätig und führte grundlegende Untersuchungen zu Planetenbewegungen durch.
Der Ausbruch des Dreißigjährigen Krieges im Jahre 1618 hat Leben und Arbeit von JOHANNES KEPLER wesentlich beeinflusst. So musste er zweimal lange Reisen in seine Heimatstadt antreten, um dort seine von den Protestanten als Hexe angeklagte Mutter vor Folter und Feuertod zu retten.
1628 trat KEPLER in die Dienste des kaiserlichen Feldherrn WALLENSTEIN, der ihm als Herzog von Mecklenburg eine Professur an der Universität in Rostock in Aussicht stellte. Ehe er diese antrat, machte sich KEPLER auf eine weite Reihe nach Regensburg, wo der Reichstag versammelt war. Hier wollte er wegen ausstehender Gehälter vorstellig werden.
Geschwächt durch die Reise starb JOHANNES KEPLER wenige Tage nach seiner Ankunft in Regensburg am 15. November 1630 im Alter von knapp 59 Jahren.
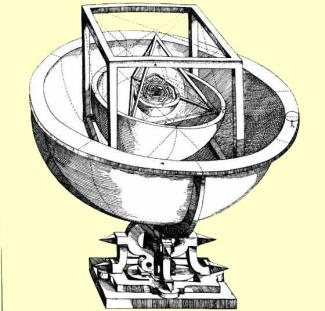
Keplers „Weltgeheimnis“ – eine Darstellung von Planetensphären, eingepasst in reguläre Körper
Zu KEPLERS wissenschaftlichen Leistungen
Bereits im Jahre 1594 entstand KEPLERS erstes astronomisches Werk, das unter dem Titel „Mysterium cosmographicum“ (Geheimnis der Weltbeschreibung) herausgegeben wurde. In diesem recht spekulativen Werk werden die geometrischen Eigenschaften regulärer Polyeder (platonischer Körper) mit den Abständen der Planetenbahnen in Verbindung gebracht und daraus der „göttliche Bauplan des Universums“ entwickelt.
Bei BRAHE beschäftigte sich KEPLER intensiv mit der Berechnung von Planetenbahnen, insbesondere der Berechnung der Marsbahn. Vor allem ging es darum, die Beobachtungsdaten BRAHEs mit den Berechnungen in Übereinstimmung zu bringen.
Im Ergebnis mehrjähriger Arbeiten erschien 1609 ein Werk unter dem Titel „Astronomia nova“ (Die neue Astronomie). In diesem Werk ist die bedeutendste wissenschaftliche Leistung KEPLERs dargestellt, indem dort die ersten beiden Gesetze der Planetenbewegung formuliert sind:
- 1. keplersches Gesetz: Die Planeten bewegen sich auf elliptischen Bahnen. In einem gemeinsamen Brennpunkt steht die Sonne.
- 2. keplersches Gesetz: Eine von der Sonne zum Planten gezogene Linie überstreicht in gleichen Zeiten gleich große Flächen.
Während KEPLER in frühen Werken als Ursache der Planetenbewegung himmlische Intelligenzen oder Seelenkräfte annahm, geht er jetzt von magnetischen Kräften aus, die die Sonne ausüben soll.
Neben Untersuchungen zu Planeten beschäftigte sich KEPLER auch mit astronomischen Instrumenten. So entwickelte er ein verbessertes Fernrohr mit zwei Sammellinsen, das wir heute als keplersches Fernrohr kennen.
Ein 1615 unter dem Titel „Nova stereometria doliorum vinariorum“ (Neue Stereometrie der Weinfässer) erschienenes Werk trug wesentlich zur Weiterentwicklung der Integralrechnung bei. KEPLER knüpfte hierin an Methoden der Volumenberechnung aus der Antike, speziell an Ergebnisse von ARCHIMEDES, an. Das Neue bestand darin, dass er dabei so genannte infinitesimale Methoden (den Begriff des unendlich Kleinen) einbezog.
Aus Kugeln, Zylindern, Kegeln und Kegelstümpfen setzte KEPLER neue Körper zusammen, so etwa das Fass aus Kreiszylinder und zwei Kreiskegelstümpfen, was ihn zu einer noch heute benutzten und nach ihm benannten Regel führte.
Die keplersche Fassregel besagt, dass ein Fass der Höhe h sowie der Grundfläche , der in der Mitte gemessenen Querschnittsfläche und der Deckfläche etwa folgendes Volumen hat:
Diese Näherungsformel liefert selbst dann noch gute Ergebnisse, wenn die Querschnittsflächen keine Kreise sind.
1619 erschienen „Die Weltharmonien“, in dem das folgende 3. keplersche Gesetz formuliert war:
- 3. keplersches Gesetz: Die Quadrate der Umlaufzeiten zweier Planeten verhalten sich wie die dritten Potenzen der großen Halbachsen ihrer Bahnen, d.h., es gilt:
Um seine grundlegenden Entdeckungen für die Astronomen nutzbar zu machen, widmete sich KEPLER in seinen letzten Lebensjahren der Aufgabe, neue astronomische Tafeln zu berechnen. Der letzte Band der nach seinem Förderer Kaiser RUDOLF II. benannten „Rudolfinischen Tafeln“ erschien in KEPLERS Todesjahr.
platonische Körper Kepler Volumenbestimmung keplersche Gesetze Polyeder keplersche Fassregel Ellipse
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 