Gewichtskraft
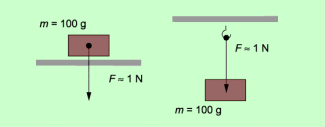
Die Gewichtskraft gibt an, wie stark ein Körper auf eine Unterlage drückt oder an einer Aufhängung zieht.
| Formelzeichen: | |
| Einheit: | ein Newton (1 N) |
Die Gewichtskraft kann mit der Gleichung berechnet werden.
Sie ist wie jede andere Kraft eine gerichtete (vektorielle) Größe. Im Unterschied zur Masse ist die Gewichtskraft vom Ort abhängig, an dem sich der betreffende Körper befindet.
Alle Körper ziehen sich aufgrund ihrer Masse gegenseitig an. Diese Erscheinung wird als Massenanziehung oder Gravitation bezeichnet. Für die Erde und die auf ihr befindlichen Körper gilt dann: Alle Körper auf der Erde werden von dieser angezogen. Diese Anziehungskraft bewirkt, dass ein Apfel, wenn man ihn loslässt, nach unten fällt. Eine Maschine drückt auf ihre Unterlage. Ein Kind, das auf einer Schaukel sitzt, bewirkt eine Zugkraft an der Aufhängung der Schaukel. Die Kraft, mit der ein Körper aufgrund seiner Masse auf eine Unterlage drückt oder an einer Aufhängung zieht, wird als Gewichtskraft bezeichnet.
Die Gewichtskraft gibt an, wie stark ein Körper auf eine Unterlage drückt oder an einer Aufhängung zieht.
| Formelzeichen: | |
| Einheit: | ein Newton (1 N) |
Die Gewichtskraft, die auf einen Körper wirkt, hängt ab
- von seiner Masse und
- von dem Ort, an dem er sich befindet.
Je größer die Masse eines Körpers ist, umso größer ist auch seine Gewichtskraft. Sie kann berechnet werden mit der Gleichung:
| m | Masse des Körpers | |
| g | Fallbeschleunigung (Ortsfaktor) |
Die Fallbeschleunigung, auch Ortsfaktor genannt, hat auf der Erdoberfläche einen mittleren Wert von:
Das bedeutet: Ein Körper der Masse 1 kg hat auf der Erdoberfläche eine Gewichtskraft von 9,81 N. Für Abschätzungen und Überschlagsrechnungen kann man mit dem Zahlenwert 10 rechnen.
Die Gewichtskraft ist wie jede andere Kraft eine gerichtete (vektorielle) Größe. Sie zeigt in Richtung Erdmittelpunkt. Im Unterschied zur Masse ist die Gewichtskraft vom Ort abhängig, an dem sich der betreffende Körper befindet.
Gewichtskraft und Masse
Wichtige Unterschiede zwischen den physikalischen Größen Masse und Gewichtskraft sind in der nachfolgenden Übersicht zusammengestellt.
![]()
Ortsabhängigkeit der Gewichtskraft
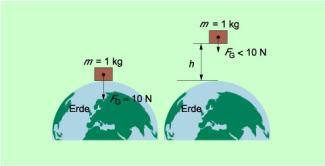
Die Gewichtskraft ist ortsabhängig. Auf der Erdoberfläche sind die Unterschiede bei der Gewichtskraft eines Körpers gering. Der Ortsfaktor schwankt zwischen 9,79 N/kg am Äquator und 9,83 N/kg an den Polen.
Je weiter ein Körper von der Erde entfernt ist, umso kleiner ist die Anziehungskraft der Erde und umso kleiner ist folglich auch seine Gewichtskraft (Bild 3). In einer Höhe von 250 km über der Erdoberfläche beträgt die Gewichtskraft eines Körpers von 1 kg Masse noch etwa 9 N, in 2 600 km Höhe noch etwa 5 N, also die Hälfte der Gewichtskraft auf der Erdoberfläche.
Für die Mondoberfläche hat der Ortsfaktor einen Wert von 1,62 N/kg. Demzufolge beträgt die Gewichtskraft auf der Mondoberfläche nur ca. 1/6 derjenigen auf der Erdoberfläche.
Auf der Oberfläche des größten Planeten unseres Sonnensystems, des Jupiters, beträgt die Gewichtskraft eines Körpers etwa 2,5-mal so viel wie auf der Erdoberfläche.