Kreis
Der Kreis ist die Menge aller Punkte der Ebene, die von einem festen Punkt M der Ebene den gleichen Abstand r haben.
M heißt Mittelpunkt, und die Strecke der Länge r, die jeden Punkt des Kreises mit seinem Mittelpunkt verbindet, heißt Radius.
Nach dieser Definition ist der Kreis eine Linie, die Kreislinie. Der Mittelpunkt M gehört nach dieser Definition nicht zum Kreis.
Alle Randpunkte und alle inneren Punkte eines Kreises bilden gemeinsam die Fläche des Kreises, die Kreisfläche.
Aus dem Zusammenhang wird meist deutlich, ob mit dem Wort „Kreis“ die Kreislinie oder die Kreisfläche gemeint ist.
Kreis
Kreis - Kreise
Kreis
egal - iStock by Getty Images
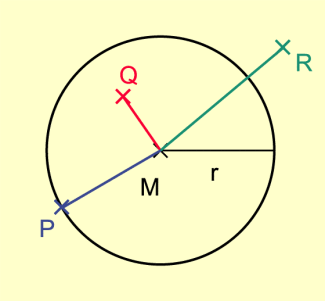
Ein Punkt heißt bezüglich eines Kreises mit dem Mittelpunkt M und dem Radius r:
– innerer Punkt Q, wenn ,
– Randpunkt P, wenn und
– äußerer Punkt R, wenn
Innere und äußere Punkte
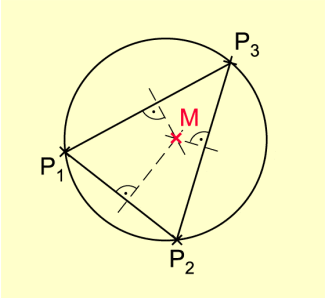
Durch drei nicht auf einer Geraden liegende Punkte lässt sich stets genau ein Kreis zeichnen. Sein Mittelpunkt ist der Schnittpunkt der Mittelsenkrechten der Verbindungsstrecken der drei Punkte.
Haben zwei Kreise drei Punkte gemeinsam, so sind die Kreise identisch.
Kreis und Symmetrie
Jeder Kreis ist achsensymmetrisch. Jede Gerade durch den Mittelpunkt des Kreises ist Symmetrieachse, somit besitzt ein Kreis unendlich viele Symmetrieachsen.
Jeder Kreis ist punkt- und drehsymmetrisch mit seinem Mittelpunkt als Symmetrie- und Drehzentrum.
Zwei Kreise
Konstruktion eines Kreises
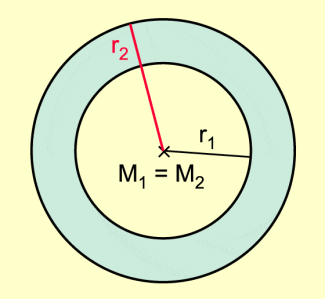
Falls für zwei Kreise und gilt, heißen die Krei se konzentrische Kreise. Die Fläche zwischen zwei konzentrischen Kreisen heißt Kreisring.
Kreisring
Ein Angebot von 