Thales
THALES VON MILET (etwa 624 bis 548 v. Chr.), ionischer Philosoph und Mathematiker (Geometer)
* um 624 v. Chr.
† um 548 v. Chr.
THALES VON MILET beschäftigte sich neben philosophischen Fragen vor allem mit geometrischen Problemen. Er bewies u. a., dass jeder Peripheriewinkel (Umfangswinkel) über dem Halbkreis ein rechter ist (Satz des Thales).
Zur Person
THALES lebte von etwa 624 bis 548 v. Chr. Die Stadt Milet, aus der er stammt, liegt im Südwesten Kleinasiens, auf heute türkischem Gebiet.
Seine Lebensdaten werden unterschiedlich angegeben; überhaupt ist bei allem, was über ihn überliefert ist, schwer zu entscheiden, was Wahrheit ist und was in den Bereich der Legende gehört. So soll THALES einem griechischen Historiker zufolge für den 28. Mai des Jahres 585 v. Chr. eine Sonnenfinsternis vorhergesagt haben, die während einer Schlacht zwischen Medern und Lydern eintrat und Einfluss auf deren Ausgang hatte. Das ist ein Hinweis auf seine Lebensdaten und zugleich ein Beweis dafür, dass er umfassende astronomische Kenntnisse besaß und wahrscheinlich auch die astronomischen Tafeln über solche Himmelsereignisse von den Babyloniern erhalten hatte.
THALES war ein Kaufmann, der durch den Handel mit Salz und Öl ein beträchtliches Vermögen erworben und dazu Reisen u. a. nach Ägypten und Babylon unternommen hatte. Das gestattete es ihm, sich mit wissenschaftlichen Problemen zu befassen. Dabei war es sein Bestreben, die Natur nicht nur zu erkennen, sondern sie auch zu erklären.
In seiner Philosophie war die Erde eine große Scheibe, die auf dem Wasser schwamm, und das war das Grundprinzip und die Quelle allen Seins. Er suchte nach natürlichen Erklärungen für die Erscheinungen, ohne sie auf Götter zurückzuführen. Er gründete die sogenannte ionische Philosophenschule. Von der Hochachtung, die er allseits genoss, zeugt die Tatsache, dass er zu den „Sieben Weltweisen“ gerechnet wurde.
Zu mathematischen Leistungen THALES'
Mit Mathematik begann sich THALES erst zu befassen, als er bereits ziemlich alt war. Auch hier sammelte er nicht nur Gesetzmäßigkeiten, sondern suchte nach Erklärungen dafür.
Der Satz, dass die Winkelsumme im Dreieck beträgt, geht auf ihn zurück. Als Begründung gab er folgenden Gedankengang an:
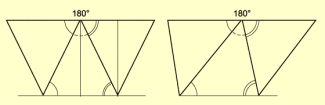
Legt man sechs gleichseitige Dreiecke (zu einem regelmäßigen Sechseck) aneinander, so bilden die Spitzen einen Vollwinkel. Jeder einzelne Winkel muss somit und die Summe von drei Winkel betragen.
Analog legte er zunächst gleichschenklige und dann ungleichseitige Dreiecke aneinander und zeigte, dass die Summe der drei Winkel stets einen gestreckten Winkel ergab (Bild 2).
Der auf THALES zurückgehende und nach ihm benannte Thalessatz wird gewöhnlich in folgender Kurzfassung angegeben:
Jeder Peripheriewinkel über dem Halbkreis ist ein rechter (Winkel).
THALES begründete diesen Satz folgendermaßen:
-
Winkelsumme im Dreieck
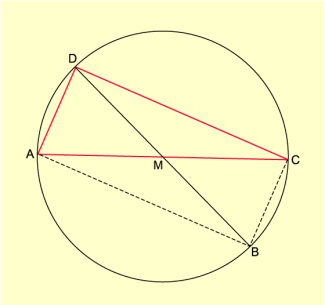
In jedem Rechteck sind die Diagonalen gleich lang und halbieren einander. Umgekehrt, folgerte er, ist ein Viereck, indem die Diagonalen gleich lang sind und einander halbieren, ein Rechteck. Zeichnet man nun in einen Kreis zwei Durchmesser AC und BD ein und verbindet man die Punkte zu einem Viereck ABCD, so hat es diese Eigenschaften, muss also ein Rechteck sein und an seinen Eckpunkten A, B, C und D liegen demzufolge rechte Winkel (Bild 3).
THALES soll auch die Entfernung von Schiffen von der Küstenlinie ermittelt haben, indem er von den Endpunkten einer Standlinie am Ufer die Winkel zwischen der Standlinie und den Sehstrahlen zu einem Schiff maß und durch eine maßstäbliche Konstruktion die Entfernung herausfand. Er benutzte dabei den Kongruenzsatz wsw, den er auch als Satz formulierte, und eigentlich auch den Hauptähnlichkeitssatz.
-
Figur zum Thalessatz
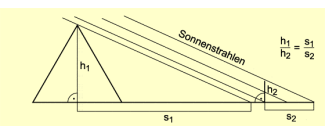
Der Ähnlichkeit von Dreiecken bediente er sich auch in einem anderen Fall. Als er in Ägypten weilte, wollten ihn die Priester auf die Probe stellen und forderten ihn auf, die Höhe einer Pyramide zu ermitteln. THALES maß daraufhin die Länge des Schattens der Pyramide, die Länge eines senkrecht von ihm in den Boden gestreckten Stabes und den Schatten, den dieser warf (Bild 4). Über eine Verhältnisgleichung berechnete er so die Höhe zum Erstaunen der Priester ziemlich genau.
THALES hat keine Aufzeichnungen hinterlassen, aber Berichte seiner Zeitgenossen und seiner Nachfahren legen Zeugnis von seinem Wirken und seinen Leistungen ab, sodass man ihn mit vollem Recht als den Stammvater der griechischen Mathematik bezeichnen darf.
-
Bestimmung der Höhe einer Pyramide