Berechnungen am Kreis
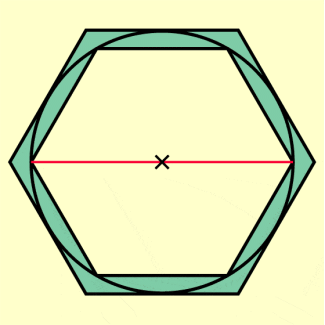
Um den Umfang u eines Kreises mit dem Durchmesser d zu bestimmen, kann man von den Umfängen eines einbeschriebenen und eines umbeschriebenen Vielecks ausgehen, z. B. eines regelmäßigen Sechsecks. Für den Umfang des Kreises gilt:
Umfang eines Kreises
Um den Umfang u eines Kreises mit dem Durchmesser d zu bestimmen, kann man von den Umfängen eines einbeschriebenen und eines umbeschriebenen Vielecks ausgehen, z. B. eines regelmäßigen Sechsecks (Bild 1). Der Umfang des einbeschriebenen Sechsecks (= 3 · d) ist kleiner, der Umfang des umbeschriebenen Sechsecks ( = 3,46 · d) ist größer als der Umfang des Kreises:
Der Faktor, mit dem man d multiplizieren muss, um u zu erhalten, ist eine der wichtigsten und interessantesten mathematischen Konstanten. Sie wird mit bezeichnet:
= 3,141592653589793238…
Näherungsweise wird oft = 3,14 verwendet.
Für den Umfang des Kreises gilt:
-
Umfang eines Kreises
Länge eines Kreisbogens
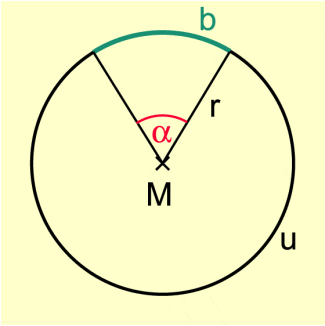
Die Länge eines Kreisbogens b hängt von der Länge des Durchmessers und von der Größe des zugehörigen Mittelpunktswinkels ab (Bild 2). Für den ganzen Kreis ist der Mittelpunktswinkel und die Länge des Bogens gleich dem Umfang, woraus sich die Proportion ergibt.
Für die Länge des zum Mittelpunktswinkel gehörenden Bogens gilt:
-
Länge eines Kreisbogens
Flächeninhalt eines Kreises
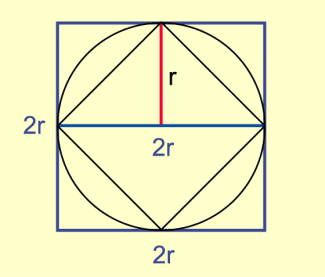
Wenn man um und in einen Kreis jeweils ein Quadrat zeichnet, kann man mithilfe dieser Quadrate den Flächeninhalt eines Kreises einschachteln (Bild 3).
Der Flächeninhalt eines Kreises liegt also zwischen und .
-
Flächeninhalt eines Kreises
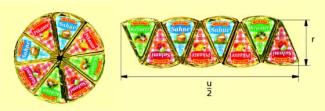
Eine weitere Möglichkeit, den Flächeninhalt des Kreises zu bestimmen, ist die Zerlegung in Teilflächen, die sich annähernd zu einem Parallelogramm mit der Grundseite und der Höhe r umlegen lassen (Bild 4).
Bei Vergrößerung der Anzahl der Teilflächen wird die Annäherung an ein Parallelogramm immer besser.
Für den Flächeninhalt A eines Kreises gilt dann:
Für eingesetzt ergibt sich:
Der Flächeninhalt eines Kreises ist das Produkt aus der Kreiszahl und dem Quadrat seines Radius r. Es gilt:
bzw.
-
Flächenumwandlung
Flächeninhalt eines Kreisausschnitts (Kreissektors)
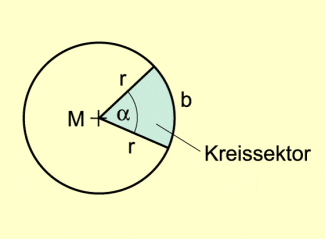
Der Teil einer Kreisfläche, der von zwei Radien r und einem Kreisbogen b begrenzt wird, heißt Kreisausschnitt (Bild 5).
Der Flächeninhalt A eines Kreisausschnitts ist proportional zu dem zugehörigen Mittelpunktswinkel , da sich bei Verdopplung von auch A verdoppelt. Der Anteil des Flächeninhalts des Kreisausschnitts A am Flächeninhalt des Kreises entspricht dem Anteil des Mittelpunktswinkels am Vollwinkel .
In einem Kreis mit dem Radius r gilt für den Flächeninhalt A eines Kreisausschnitts mit dem dazugehörigen Mittelpunktswinkel :
-
Flächeninhalt eines Kreissektors
Flächeninhalt eines Kreisabschnitts (Kreissegments)
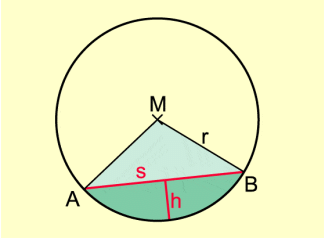
Der Flächeninhalt des Kreisabschnitts ergibt sich aus der Differenz der Flächeninhalte des Kreisausschnitts und des Dreiecks ABM (Bild 6):
-
Flächeninhalt eines Kreisabschnitts
Flächeninhalt eines Kreisrings
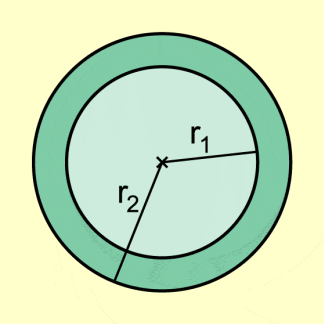
Für den Flächeninhalt eines Kreisrings gilt (Bild 7):
-
Flächeninhalt eines Kreisrings