Kubische Gleichungen, grafisches Lösen

Bei einem grafischen Näherungsverfahren geht man wie folgt vor: Man betrachtet die Funktion $y=f\left(x\right)=x^3+a{x}^2+bx+c$. Weil diese Funktion stets mindestes einmal die x-Achse schneidet (also eine reelle Nullstelle hat), wird diese durch Näherungsverfahren (z. B. Regula falsi oder Intervallschachtelung) verbessert, bis eine gewünschte Genauigkeit erreicht ist und die Gleichung dann durch Polynomdivision auf eine quadratische zurückgeführt werden kann.

Eine grobe Näherungslösung einer kubischen Gleichung erhält man dadurch, dass man die Gleichung, nachdem sie mithilfe der Substitution $x=z-\frac{a}{3}$ in die reduzierte Form $z^3+pz+q=0$ (bzw. $x^3+px+q=0$) gebracht wurde, in zwei Funktionen zerlegt.
Aus $x^3+px+q=0$ folgt $x^3=-px-q$, und man betrachtet deshalb folgende Funktionen:
$\begin{array}{l}y=f_1\left(x\right)=x^3\\ y=f_2\left(x\right)=-px-q\end{array}$
Die Graphen dieser Funktionen werden in ein Koordinatensystem eingetragen, die Abszisse der Schnittstelle (des Schnittpunktes der Graphen) ist eine (mit Ablesefehler belastete) Näherung für eine reelle Lösung. Sie kann – falls erforderlich – durch Näherungsverfahren verbessert werden.

Beispiel 1:
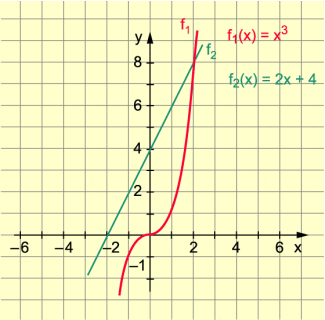
Die Gleichung $x^3-2x-4=0$ soll näherungsweise grafisch gelöst werden.
$\begin{array}{l}{x}^3=2x+4\Rightarrow y=f_1\left(x\right)=x^3\\ y=f_2\left(x\right)=2x+4\end{array}$
Der Darstellung der Funktionsgraphen in Bild 1 entnimmt man als Lösung x = 2.

Beispiel 2:
Die Gleichung $x^3-4x+4=0$ ist grafisch zu lösen.
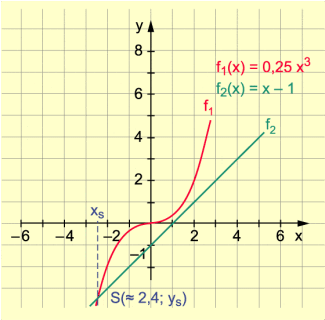
Hier empfiehlt es sich, die Graphen der zu betrachtenden Funktionen zu stauchen, etwa durch Multiplikation mit 0,25. Man erhält folgende äquivalente Gleichung:
$\mathrm{0,25}{x}^3-x+1=0$
Als Abszisse des Schnittpunktes der Graphen von $y=f_1\left(x\right)=\mathrm{0,25}{x}^3$ und $y=f_2\left(x\right)=x-1$ erhält man $x\approx -\mathrm{2,4}$ (Bild 2).
Da bei der gegebenen Gleichung das quadratische Glied fehlt, könnte zur Lösung auch sofort die cardanische Formel mit $p=-4$und $q=4$ benutzt werden. Es ist (wegen der Eineindeutigkeit der Funktion $y=x^3$):

$\begin{array}{l}x=\sqrt[3]{-2+\sqrt{4-\frac{64}{27}}}+\sqrt[3]{-2-\sqrt{4-\frac{64}{27}}}\\ \approx \sqrt[3]{-2+\mathrm{1,2766}}+\sqrt[3]{-2-\mathrm{1,2766}}\\ \approx -\mathrm{0,8977}-\mathrm{1,4853}\\ \approx -\mathrm{2,383}\approx -\mathrm{2,38}\end{array}$
Durch Polynomdivision erhält man ein quadratisches Polynom:
$\begin{array}{l}\left(\mathrm{0,25}{x}^3-x+1\right):\left(x+\mathrm{2,38}\right)=\mathrm{0,25}{x}^2-\mathrm{0,595}x+\mathrm{0,416}\\ -(\underset{¯}{\mathrm{0,25}{x}^3-\mathrm{0,595}{x}^2})\\ -\mathrm{0,595}{x}^2-x\\ -(\underset{¯}{-\mathrm{0,595}{x}^2-\mathrm{1,416}x})\\ \mathrm{0,416}x+1\\ -(\underset{¯}{\mathrm{0,416}x+\mathrm{0,99}})\\ \mathrm{0,01}\approx 0\end{array}$

Es ist noch die quadratische Gleichung $\mathrm{0,25}{x}^2-\mathrm{0,595}x+\mathrm{0,416}=0$ zu lösen. Diese quadratische Gleichung hat keine Nullstellen in der Menge der reellen Zahlen.
Auch den Funktionsgraphen war zu entnehmen, dass beiden Graphen keine weiteren reellen Punkte gemeinsam sind.