Mengen, Mächtigkeit
Zwei Mengen A und B sind zueinander gleichmächtig (A ~ B), wenn es eine eineindeutige Abbildung von A auf B gibt.
Jedem Element von A kann also genau ein Element von B und zugleich jedem Element von B genau ein Element von A zugeordnet werden.
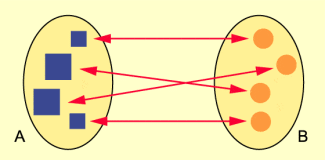
Zwei Mengen A und B sind zueinander gleichmächtig (A ~ B), wenn es eine eineindeutige Abbildung von A auf B gibt (Bild 1).
Jedem Element von A kann also genau ein Element von B und zugleich jedem Element von B genau ein Element von A zugeordnet werden.
Zwei endliche Mengen sind zueinander gleichmächtig, wenn sie die gleiche Anzahl von Elementen besitzen.
Durch paarweise Zuordnung der Elemente können auch Mengen mit unendlich vielen Elementen nach ihrer Mächtigkeit verglichen werden.
Ist eine unendliche Menge zur Menge der natürlichen Zahlen gleichmächtig, so ist sie eine abzählbar unendliche Menge.
Anderenfalls ist die Menge überabzählbar unendlich.
Beispiel:
Eine exakte Definition der reellen Zahlen und des Rechnens mit diesen Zahlen gelang den deutschen Mathematikern KARL WEIERSTRASS (1815 bis 1897) und GEORG CANTOR (1845 bis 1918). CANTOR hat auch als Erster bewiesen, dass die Menge der irrationalen Zahlen viel mächtiger als die Menge der rationalen Zahlen ist.
-
Zueinander gleichmächtige Mengen A und B
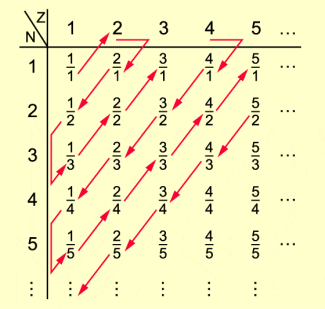
CANTOR bewies, dass man die rationalen Zahlen abzählen kann. Er dachte sich dazu das folgende Abzählverfahren aus: In dem abgebildeten unendlichen Schema (Bild 2) sind alle Brüche und damit alle gebrochenen Zahlen außer der 0 enthalten. Wenn man das Schema längs der eingezeichneten Diagonalen durchläuft, werden nacheinander alle Brüche einmal erfasst. Man kann also die Brüche auf diese Art durchnummerieren, d. h., man kann sie abzählen. Im Gegensatz dazu gibt es kein Verfahren, mit dem man die Menge der reellen Zahlen abzählen kann.
Sie ist „überabzählbar“, man sagt auch, sie hat eine größere Mächtigkeit als die Menge der rationalen Zahlen.
-
Abzählbarkeit der gebrochenen Zahlen