Periodizität von Funktionen

Beispiel 1:
Ein Kondensator möge in 3 s eine Ladung von 2 C aufnehmen und sich durch eine geeignete Schaltung dann (praktisch „schlagartig“) entladen, wonach der gleiche Prozess wieder beginnt.

Beispiel 2:
Jonas legt von seinem Taschengeld und dem (leider „unregelmäßigen“) Zuverdienst jeden Tag 10 ct in eine Sparbüchse. Haben sich nach 100 Tagen jeweils $1000ct=10€$ angesammelt, so zahlt Jonas diesen Betrag auf sein Konto ein.

Unabhängig vom konkreten Inhalt werden die in den beiden Beispielen geschilderten Vorgänge grob betrachtet (und ohne Rücksicht auf „Lücken“) durch Graphen der folgenden Art beschrieben:

Die Funktionswerte wachsen jeweils an, und wenn eine Grenzhöhe G (der Ladung bzw. des Sparbüchseninhalts) erreicht ist, gehen sie auf einen bestimmten Wert (hier 0 C bzw. 0 ct) zurück. Anschließend beginnt der Prozess in der gleichen Weise von Neuem und erreicht im Abstand t (von 3 s bzw. 100 Tagen) immer wieder dieselbe Höhe g (denselben Wert).

Eine Verallgemeinerung der obigen Überlegungen führt uns zum Begriff der Periodizität:

Eine Funktion f heißt periodische Funktion, wenn es eine Zahl b (mit b > 0) gibt, sodass mit x auch x + b zum Definitionsbereich D gehört und für jedes $x\in D$ gilt:
$f\left(x\right)=f\left(x+b\right)$
Die kleinste derartige Zahl b wird Periode von f genannt.

Das heißt z. B.:
– Im Abstand von b wiederholen sich die Funktionswerte von f.
– Die Abschnitt des Graphen von f über den Intervallen $\left[\text{x;}\text{x}+\text{b}\right]$, $\left[\text{x}+\text{b};\text{x}+\text{2b}\right]$, $\left[\text{x}+\text{2b;}\text{x}+\text{3b}\right]$ aus D sind kongruent.

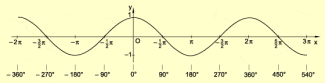
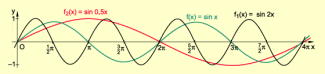
Eine wichtige Klasse periodischer Funktionen sind die Winkelfunktionen. Beispielsweise besitzt die Funktion $f\left(x\right)=\sin x$ die Periode $2\pi$, die Funktion $f_2\left(x\right)=\sin \mathrm{0,5}x$ die Periode $4\pi$ und die Funktion $f_3\left(x\right)=\sin 2x$ die Periode $\pi$ (Bild 1).

Die Funktion $f\left(x\right)=\cos x$ (Bild 2) besitzt mit $2\pi$ die gleiche Periode wie $f\left(x\right)=\sin x$.