Prismatoid

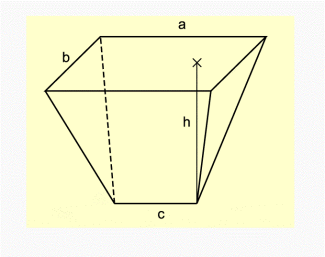
Ein Prismatoid (Prismoid) ist ein ebenflächig begrenzter Körper mit parallelen Grund- und Deckenflächen sowie mit Dreiecken oder Trapezen als Seitenflächen. Im Unterschied zum Prisma brauchen Grund- und Deckfläche nicht kongruent zu sein und auch nicht die gleiche Eckenzahl zu haben.

Das Volumen eines Prismatoids lässt sich nach der Formel

$V=\frac{h}{6}\left(A_G+4A_S+A_D\right)$

berechnen. Dies ist eine der berühmtesten und universellsten Volumenformeln. Zu Ehren ihres Entdeckers heißt sie keplersche Fassregel.

KEPLER fand diese Formel im Jahre 1613 als er sich mit der Geometrie von Weinfässern beschäftigte. Der Anlass für seine Untersuchungen war wie bei vielen anderen mathematischen Entdeckungen auch ein praktisches Problem. Er wollte die traditionelle Methode der Weinbauern, das Volumen der Fässer mit einer hineingesteckten Messrute zu bestimmen, erforschen und verbessern.
KEPLER schreibt in der Vorrede seines 1615 erschienenen Buches „Nova stereometria doliorum vinariorum“ (Neue Stereometrie der Weinfässer):
„Als ich im November des letzten Jahres (1613) meine Wiedervermählung feierte, zu einer Zeit, da an den Donauufern bei Linz die aus Niederösterreich herbeigeführten Weinfässer nach einer reichlichen Lese aufgestapelt und zu einem annehmbaren Preis zu kaufen waren, da war es die Pflicht des neuen Gatten und fürsorglichen Familienvaters, für sein Haus den nötigen Trunk zu besorgen. Als einige Fässer eingekellert waren, kam am vierten Tag der Verkäufer mit der Messrute, mit der er alle Fässer, ohne Rücksicht auf ihre Form, ohne jede weitere Überlegung oder Rechnung ihrem Inhalt nach bestimmte ... Ich bezweifelte die Richtigkeit der Methode, denn ein sehr niedriges Fass mit etwas breiteren Böden und daher sehr viel kleinerem Inhalt könnte dieselbe Visierlänge besitzen. Es schien mir als Neuvermähltem nicht unzweckmäßig, ein neues Prinzip mathematischer Arbeiten, nämlich die Genauigkeit dieser bequemen und allgemein wichtigen Bestimmungen nach geometrischen Grundsätzen zu erforschen und die etwa vorhandenen Gesetze ans Licht zu bringen.“
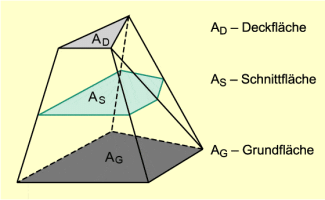
KEPLER fand die Lösung des Problems in drei Tagen. Sein Grundgedanke war, das Fass durch eine Folge ebenflächig begrenzter Körper möglichst genau anzunähern. Dazu verwendete er Prismatoide.

Mit der keplerschen Fassregel kann ebenfalls das Volumen eines Quaders, Prismas, eines Zylinders, einer Pyramide, eines Kegels, eines Pyramiden- oder Kegelstumpfes, einer Kugel und vieler weiterer Körper berechnet werden. So ist sie auch zur Volumenbestimmung eines Obelisken bzw. eines Pontons oder eines Keils anwendbar.
Bei einem Keil ergibt sich damit folgende Volumenformel:
$V=\frac{h}{6}b\left(2a+c\right)$