Mathematik
Klasse
8-9
Winkel am Kreis
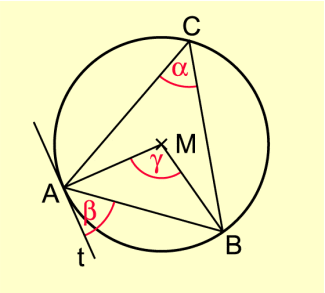
Ein Winkel heißt Mittelpunktswinkel (Zentriwinkel), wenn sein Scheitel im Kreismittelpunkt liegt, Umfangswinkel (Peripheriewinkel), wenn sein Scheitel auf dem Kreis liegt und seine Schenkel den Kreis schneiden, Sehnen-Tangenten-Winkel, wenn sein Scheitel auf dem Kreis liegt und ein Schenkel den Kreis schneidet, der andere den Kreis berührt (Bild 1).
Winkel am Kreis
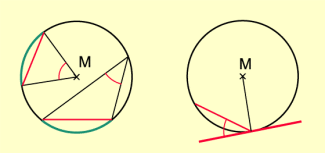
Zu jedem Mittelpunkts- und jedem Umfangswinkel gehören eine bestimmte Sehne und ein bestimmter Kreisbogen.
Alle Umfangswinkel über demselben Bogen sind gleich groß (Bild 2) .
Beweisidee:
, usw. sind Sehnenvierecke. Die Winkel in B und , in B und usw. ergänzen sich zu .
Häufig verwendet man statt „über demselben Bogen“ den Ausdruck „über derselben Sehne“. Dabei muss allerdings beachtet werden, dass zu jeder Sehne, die nicht Durchmesser ist, stets zwei verschiedene Kreisbögen und somit auch zwei verschieden große Umfangswinkel gehören.
Diese gegenüberliegenden Umfangswinkel ergänzen sich zu .
Jeder Umfangswinkel über einem Halbkreis (bzw. über dem Durchmesser eines Kreises) ist ein rechter Winkel (Satz des Thales).
Die Umkehrung des Satzes des Thales lautet wie folgt:
Die Scheitelpunkte aller rechten Winkel, deren Schenkel durch A und B verlaufen, liegen auf dem Kreis mit dem Durchmesser AB.
Umfangswinkel
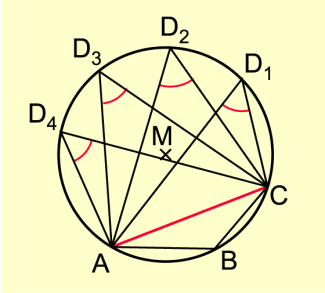
Ein Mittelpunkts- und ein Umfangswinkel heißen einander zugehörig, wenn sie über derselben Sehne liegen und ihre Scheitel auf derselben Seite der Sehne, also über demselben Bogen liegen.
Zu allen Umfangswinkeln über einem Bogen gehört ein Mittelpunktswinkel.
Es gilt der Mittelpunkts-Umfangswinkel-Satz:
Jeder Umfangswinkel über demselben Bogen ist halb so groß wie der zugehörige Mittelpunktswinkel (Bild 3).
Mittelpunkts-Umfangswinkel-Satz
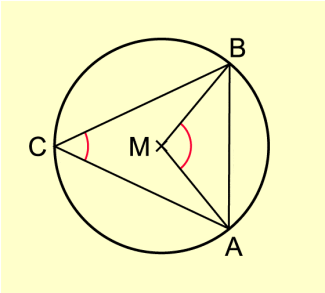
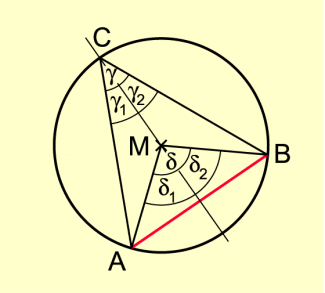
Bewiesen wird der Satz für den Fall, dass der Mittelpunkt des Kreises im Inneren des Umfangswinkels liegt (Bild 4).
Voraussetzung:
A, B und C liegen auf dem Kreis um M; M liegt im Innern von
Behauptung:
Beweis:
Die Gerade durch C und M teilt und .
Es gilt: und (Basiswinkel in den gleichschenkligen Dreiecken AMC bzw. MBC)
Es gilt: (Außenwinkelsatz)
Daraus folgt oder
Für die anderen beiden Fälle (M liegt auf einem Schenkel bzw. außerhalb des Umfangswinkels) verläuft der Beweis analog.
Beweisfigur zum Mittelpunkts-Umfangswinkel-Satz
- Jeder Sehnen-Tangenten-Winkel ist halb so groß wie der zugehörige Mittelpunktswinkel.
- Jeder Sehnen-Tangenten-Winkel ist so groß wie der zugehörige Umfangswinkel (Bild 5).
Sehnen-Tangenten-Winkel
Ein Angebot von 