Sehnenviereck
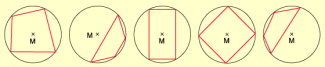
Besitzt ein Viereck einen Umkreis, so nennt man es Sehnenviereck (Bild 1).
Alle gleichschenkligen Trapeze, alle Rechtecke und damit auch alle Quadrate besitzen einen Umkreis.
Unter dem Umkreis eines n-Ecks versteht man den Kreis, der durch alle Eckpunkte des n-Ecks geht. Die Seiten des n-Ecks sind Sehnen des Umkreises.
Für alle Sehnenvierecke gilt folgender Satz:
Die Summe gegenüberliegender Winkel im Sehnenviereck ist 180°.
Sehnenvierecke
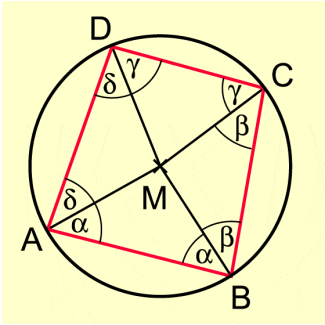
Bewiesen wird der Satz für den Fall, dass der Mittelpunkt des Umkreises innerhalb des Sehnenvierecks liegt (Bild 2).
Voraussetzung:
A, B, C und D liegen auf einem Kreis um M, d. h.
Behauptung:
Beweis:
In den gleichschenkligen Dreiecken ABM, BCM, CDM und DAM sind die Basiswinkel paarweise zueinander kongruent.
Dann ist und auch .
Da die Innenwinkelsumme im Viereck ist, gilt , also . (w. z. b. w.)
Beweisfigur
Für die anderen beiden Fälle (M liegt auf einer Seite des Sehnenvierecks oder außerhalb des Sehnenvierecks) verläuft der Beweis analog.
Alle regelmäßigen Vielecke besitzen einen Umkreis, was häufig zu ihrer Konstruktion verwendet wird.
In einen Umkreis gezeichnete Vielecke heißen einbeschriebene Vielecke.
Rechteck Sehne Viereck Berechnung Sehnenviereck Umkreis einbeschrieben Trapez Quadrat Rechenbeispiel Excel-Beispiel
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 