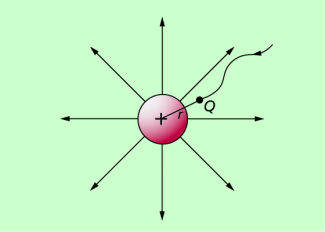
Arbeit und Energie im elektrischen Feld

Befinden sich elektrisch geladene Körper oder Teilchen im elektrischen Feld und sind sie frei beweglich, so wirkt auf sie eine Feldkraft, die Arbeit an diesen Körpern bzw. Teilchen verrichtet. Will man umgekehrt geladene Körper oder Teilchen im Feld bewegen, so muss Arbeit verrichtet werden, wenn die Bewegung entgegen der Feldkraft erfolgen soll. Die erforderliche Feldkraft kann bei einfachen Feldformen berechnet werden.
Wird an geladenen Körpern oder Teilchen mechanische Arbeit verrichtet, so ändert sich ihre Energie. Dabei gilt für den Zusammenhang zwischen Arbeit und Energie der allgemeine Zusammenhang $W = Δ E$ .

Befinden sich elektrisch geladene Körper oder Teilchen (Elektronen, Protonen oder Ionen) im elektrischen Feld, so wirkt auf sie eine Feldkraft, die berechnet werden kann mit der Gleichung $F = Q \cdot E,$ wobei Q die Ladung des Körpers oder Teilchens und E die Feldstärke im betreffenden Punkt ist.
Will man eine solche Ladung bewegen, so ist eine Kraft erforderlich, die den gleichen Betrag wie die Feldkraft hat, ihr aber entgegengerichtet ist (Bild 1). Es wird dann Arbeit im elektrischen Feld verrichtet.
Ist dagegen ein geladener Körper oder ein geladenes Teilchen im Feld und frei beweglich, so bewirkt die Feldkraft eine Bewegung, die je nach dem Vorzeichen der Ladung in Richtung oder entgegengesetzt zur Richtung des Feldes verlaufen kann. Es wird durch das Feld Arbeit am geladenen Körper oder am geladenen Teilchen verrichtet. Dadurch ändert sich jeweils die Energie des Körpers oder Teilchens.

Bei der Bewegung eines geladenen Körpers oder Teilchens im elektrischen Feld wird Arbeit verrichtet. Dabei ändert sich die Energie des Körpers oder Teilchens.

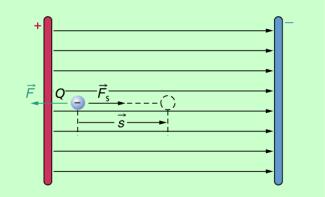
Arbeit im homogenen elektrischen Feld

In einem homogenen elektrischen Feld ist die Feldkraft konstant. Für die verrichtete mechanische Arbeit gilt unter der Voraussetzung einer konstanten Kraft in Wegrichtung:
$\begin{array}{l} W = F \cdot s \\ Mit F = Q \cdot E erhält man: \\ W = Q \cdot E \cdot s \\ Der Term E \cdot s ist die Spannung zwischen Ausgangspunkt \\ und Endpunkt, sodass man auch schreiben kann: \\ W = Q \cdot U \\ Q bewegte Ladung \\ U Spannung zwischen Anfangs- und Endpunkt \end{array}$

Dabei ist zu beachten, dass die Arbeit nur vom Anfangs- und Endpunkt der Bewegung im elektrischen Feld abhängig ist, nicht aber vom Weg, der zwischen Anfangs- und Endpunkt zurückgelegt wird.
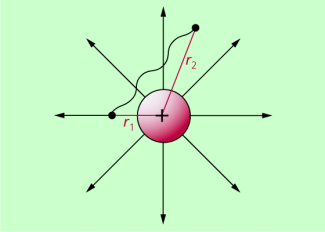
In einem beliebigen Feld ist die Feldkraft nicht konstant, die Arbeit kann demzufolge nicht in der genannten einfachen Weise berechnet werden. Liegt ein Radialfeld vor (Bild 2), dann ist eine Berechnung folgendermaßen möglich: Ausgangspunkt ist die allgemeine Definition der Arbeit in der Form:
$\begin{array}{l} W = \int_{r_{1}}^{r_{2}} F (r) d r \\ Für die Kraft F auf einen geladenen Körper im elektrischen \\ Feld gilt das coulombsche Gesetz: \\ F (r) = \frac{1}{4 π \cdot ε_{0} \cdot ε_{r}} \cdot \frac{Q_{1} \cdot Q_{2}}{r^{2}}, wobei z . B . Q_{1} die felderzeugende \\ Ladung und Q_{2} die Ladung im Feld ist . \\ Setzt man diese Gleichung in die allgemeine Definition der \\ Arbeit ein, so erhält man: \\ W = \frac{Q_{1} \cdot Q_{2}}{4 π \cdot ε_{0} \cdot ε_{r}} \cdot \int_{r_{1}}^{r_{2}} \frac{1}{r^{2}} d r = \frac{Q_{1} \cdot Q_{2}}{4 π \cdot ε_{0} \cdot ε_{r}} (\frac{1}{r_{1}} - \frac{1}{r_{2}}) \end{array}$
Auch in diesem Falle ist die Arbeit nur vom Anfangs- und Endpunkt und nicht vom Weg abhängig, der zwischen diesen beiden Punkten zurückgelegt wird.

Bewegung eines geladenen Körpers oder Teilchens in einem Radialfeld

Energie im elektrischen Feld

Betrachtet wird hier vorrangig die Energie von geladenen Körpern oder Teilchen im Feld, die nicht mit der Feldenergie, also der im elektrischen Feld gespeicherten Energie, verwechselt werden darf.
Wird an geladenen Körpern oder Teilchen mechanische Arbeit verrichtet, so ändert sich ihre Energie. Dabei gilt für den Zusammenhang zwischen Arbeit und Energie der allgemeine Zusammenhang $W = Δ E$ .
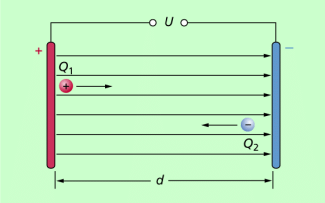
Betrachtet man einen geladenen Körper oder ein geladenes Teilchen im homogenen elektrischen Feld (Bild 3) und geht man davon aus, dass die Anfangsenergie null ist, dann erhält man bei der Bewegung zwischen zwei Punkte, zwischen denen die Spannung U besteht:
$\begin{array}{l} E = Q \cdot U oder für den speziellen Fall Q = e \\ E = e \cdot U \end{array}$
Beträgt die Spannung 1 V, so hätte ein Elektron (oder ein Proton) nach Durchlaufen dieser Spannung eine Energie von:
$\begin{array}{l} E = 1,602 \cdot 10^{- 19} C \cdot 1 V oder \\ E = 1,602 \cdot 10^{- 19} J \end{array}$
Das entspricht genau einem Elektronenvolt (1 eV).
Im beschriebenen Fall wird durch das Feld Arbeit verrichtet. Der geladene Körper bzw. das geladenen Teilchen hat dann kinetische Energie. Nach dem Energieerhaltungssatz verringert sich die Feldenergie um diesen Betrag.

Energie im homogenen elektrischen Feld

Verrichtet man an einem geladenen Körper oder Teilchen im elektrischen Feld eine Arbeit entgegen der Feldkraft, dann vergrößert sich die potenzielle Energie des Körpers bzw. Teilchens. Im homogenen Feld lässt sich diese Energie so berechnen, wie das oben beschrieben ist.
Bei beliebigen elektrischen Feldern wählt man als Bezugspunkt für die potenzielle Energie meist einen Punkt im Unendlichen und betrachtet die Arbeit an einem positiv geladenen Körper (Bild 4). Dann gilt für die potenzielle Energie allgemein:
$E_{p o t} = - Q \int_{\infty}^{r} E (r) d r$

Energie in einem Radialfeld

Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.

Verwandte Lernkarten Verwandte Klausuren

Verwandte Artikel

Arbeit und Energie im elektrischen Feld

Arbeit im homogenen elektrischen Feld

Energie im elektrischen Feld

Rechtliches

Einloggen