Das huygenssche Prinzip
Das huygenssche Prinzip ist sowohl auf elektromagnetische Wellen einschließlich Lichtwellen als auch auf mechanische Wellen anwendbar. Wir betrachten nachfolgend einige Beispiele für seine Anwendung.
Geradlinige Ausbreitung von Wellen
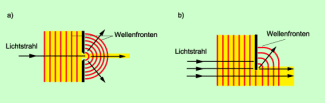
Die Ausbreitung von Wellen kann man mithilfe von Wellenfronten darstellen (Bilder 1 und 2). Die Senkrechte zu den Wellenfronten wird als Wellennormale bezeichnet. Jeder Punkt einer Wellenfront ist Ausgangspunkt von Elementarwellen (in Bild 2 grün gezeichnet). Die Resultierende oder Einhüllende aller dieser Elementarwellen ergibt die neue Wellenfront. Betrachtet man in Bild 2 statt der wenigen ausgewählten Punkt beliebig viele, so ergibt sich als Resultierende wieder eine lineare Wellenfront.
Die Resultierende aus vielen Elementarwellen bildet die neue Wellenfront.
Reflexion und Brechung von Wellen
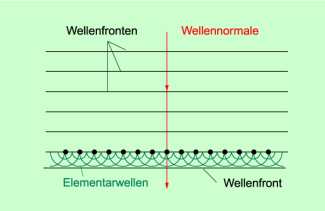
Trifft eine Wellenfront auf ein Hindernis, so ist nach dem huygensschen Prinzip jeder Punkt, der von einer Wellenfront getroffen wird, Ausgangspunkt einer Elementarwelle (Bild 3).
Trifft nun die Wellenfront schräg auf ein undurchlässiges Hindernis (Bild 3a), so gehen zunächst von Punkt 1, dann von Punkt 2 usw. Elementarwellen aus. Die Überlagerung aller Elementarwellen ergibt die neue Wellenfront. Durch eine geometrische Konstruktion kann man leicht nachweisen, dass bei einer solchen Reflexion der Reflexionswinkel gleich dem Einfallswinkel der Welle ist. Dabei wird davon ausgegangen, dass die Ausbreitungsgeschwindigkeit der Elementarwellen gleich der der Wellen ist.
Ähnlich ist der Sachverhalt auch dann, wenn Wellen auf die Grenzfläche zwischen zwei Stoffen treffen und sich in den zweiten Stoff ausbreiten können (Bild 3b), wenn also Brechung auftritt. Auch in diesem Falle ist jeder Punkt der Grenzfläche, auf den eine Welle trifft, Ausgangspunkt von Elementarwellen, die sich überlagern. Da im zweiten Stoff in der Regel die Ausbreitungsgeschwindigkeit eine andere als in Stoff 1 ist, tritt Brechung auf.
Reflexion (a) und Brechung (b) von Wellen
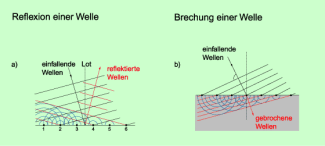
Beugung von Wellen
Treffen Wellen auf einen schmalen Spalt (Bild 4a) oder auf ein Hindernis (Bild 4b), dann breiten sich Wellen hinter dem Spalt oder Hindernis in den Raum hinein aus, wenn auch zumeist mit deutlich geringerer Intensität. Die Erklärung dafür gibt das huygenssche Prinzip: Jeder Punkt des Spaltes bzw. jeder Punkt am Hindernis ist Ausgangspunkt von Elementarwellen, die sich auch in den „Schattenraum“ hinein ausbreiten und sich zu neuen Wellenfronten überlagern.
Ein typisches Beispiel für die Beugung von Wellen kann man täglich feststellen: Geräusche, Musik oder Sprache hört man auch, wenn man sich hinter einer Hausecke, einer nicht geschlossenen Tür oder in einem anderen Raum befindet. Ursache dafür ist die Beugung, manchmal auch die Reflexion von Schallwellen.
Das huygens-fresnelsche Prinzip
Der französische Naturforscher AUGUSTIN JEAN FRESNEL (1788-1827) hat das besonders für die Erklärung optischer Erscheinungen wichtige huygenssche Prinzip mit der Interferenz in Verbindung gebracht und es damit erweitert. Man nennt es huygens-fresnelsches Prinzip. Es lautet:
Der Schwingungszustand in einem beliebigen Punkt eines Wellenfeldes wird durch alle Elementarwellen bestimmt, die von einer beliebigen Wellenfront ausgehen. Den betreffenden Schwingungszustand erhält man, wenn man in dem Punkt alle Elementarwellen unter Berücksichtigung ihrer Phasen addiert.
Mithilfe dieses Prinzips kann man z.B. erklären, warum an einem Raumbereich Verstärkung, Abschwächung bzw. Auslöschung, also typische Interferenzmuster, auftreten. Nähere Erläuterungen dazu sind unter dem Stichwort „Interferenz“ zu finden.
Beugung an einem schmalen Spalt (a) und an einem Hindernis (b)
Wellennormale Christiaan Huygens Interferenzmuster Beugung Brechung huygenssches Prinzip Wellenfront Interferenz Hindernis Spalt Ausbreitung von Wellen Reflektion Gitter Elementarwellen huygens-fresnelsches Prinzip Augustin Jean Fresnel
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 