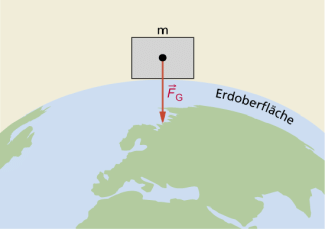
Fallbeschleunigung oder Ortsfaktor

Die Beschleunigung, die bei einem frei fallenden Körper auftritt, wenn der Luftwiderstand vernachlässigbar klein ist, wird als Fallbeschleunigung g bezeichnet. Für den mittleren Wert an der Erdoberfläche gilt:

$g=\mathrm{9,806}65\frac{\text{m}}{{\text{s}}^{\text{2}}}\approx \mathrm{9,81}\frac{\text{m}}{{\text{s}}^{\text{2}}}$

Häufig wird mit dem Näherungswert $g\approx 10\frac{\text{m}}{{\text{s}}^{\text{2}}}$ gerechnet.

Die Fallbeschleunigung, manchmal für die Erde auch Erdbeschleunigung genannt, ist abhängig von dem Ort, an dem man sich befindet. Sie wird deshalb manchmal auch als Ortsfaktor g bezeichnet und in der Einheit N/kg angegeben. Dabei gilt als mittlerer Wert für die Erdoberfläche:$g=\mathrm{9,81}\frac{\text{m}}{{\text{s}}^{\text{2}}}=\mathrm{9,81}\frac{\text{N}}{\text{kg}},\text{denn 1}\frac{\text{N}}{\text{kg}}=\frac{1\frac{\text{kg}\cdot \text{m}}{{\text{s}}^{\text{2}}}}{\text{1}\text{kg}}=1\frac{\text{m}}{{\text{s}}^{\text{2}}}$

Der Ortsfaktor gibt somit auch an, wie groß der Quotient aus der Gewichtskraft eines Körpers und seiner Masse an dem jeweiligen Ort ist. Für die Erdoberfläche bedeutet das: Ein Körper der Masse 1 kg hat eine Gewichtskraft von 9,81 N oder von etwa 10 N. Diese Zusammenhänge ergeben sich aus der Gleichung für die Gewichtskraft, die lautet:

$F_{\text{G}}=m\cdot g$

Unterschiedliche Orte - unterschiedliche Werte

Die Fallbeschleunigung hat an verschiedenen Orten unterschiedliche Werte. Nachfolgend sind einige dieser Werte angegeben.

Bestimmung der Fallbeschleunigung

Die Fallbeschleunigung kann experimentell in unterschiedlicher Weise bestimmt werden. Nachfolgend sind die wichtigsten Möglichkeiten genannt.

1. Möglichkeit: Bestimmung der Fallbeschleunigung unter Nutzung des Weg-Zeit-Gesetzes des freien Falls: $\begin{array}{l}\text{Aus}s=\frac{g}{2}{t}^2\text{ergibt sich durch Umstellung nach}g\text{die Gleichung:}\\ g=\frac{2s}{t^2}\end{array}$

Misst man den Fallweg s und die Fallzeit t, so kann man daraus die Fallbeschleunigung g berechnen. Eine mögliche Experimentieranordnung zeigt Bild 1.

2. Möglichkeit: Bestimmung der Fallbeschleunigung unter Nutzung der Gesetze für ein Fadenpendel:
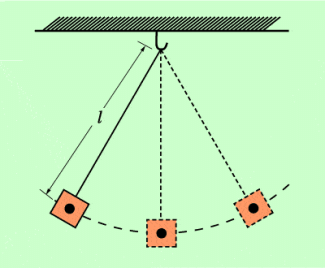
Für ein Fadenpendel (Bild 2) gilt für kleine Auslenkungen für die Schwingungsdauer T die Gleichung:

$T=2\pi \cdot \sqrt{\frac{l}{g}}$

Dabei bedeuten l die Länge des Pendels und g die Fallbeschleunigung. Stellt man diese Gleichung für die Schwingungsdauer nach der Fallbeschleunigung g um, so erhält man:

$g=\frac{4{\pi }^2\cdot l}{T^2}$

Die Pendellänge l und die Schwingungsdauer T können gemessen werden. Aus den Messwerten lässt sich die Fallbeschleunigung berechnen.

3. Möglichkeit: Die Fallbeschleunigung kann auch aus Masse und Gewichtskraft an einem bestimmten Ort ermittelt werden. Aus der Gleichung
$\begin{array}{l}F=m\cdot g\\ \text{erhält man durch Umstellen:}\\ g=\frac{F}{m}\end{array}$
Masse m eines Körpers und seine Gewichtskraft F können gemessen und damit g berechnet werden. In diesem Falle erhält man als Einheit N/kg.