Geladene Teilchen in elektrischen Feldern

Auf ein geladenes Teilchen wirkt im elektrischen Feld eine Kraft, die zur Beschleunigung des Ladungsträgers führt. Die Bahnkurve des Teilchens ist abhängig von der Richtung der Anfangsgeschwindigkeit. Bei einer Bewegung in Richtung oder entgegen der Richtung der Feldlinien erfolgt eine gleichmäßig beschleunigte Bewegung. Das wird z.B. genutzt, um schnelle Elektronen (einen Elektronenstrahl) zu erzeugen. Verläuft die Bewegung senkrecht zu den Feldlinien eines homogenen Feldes, dann bewegen sich die Ladungsträger auf einer parabelförmigen Bahn. Diese Ablenkung von der ursprünglichen geradlinigen Bewegung wird in Elektronenstrahlröhren zur Erzeugung von Bildern (z. B. bei Oszillografen) genutzt.

Induktion

#Induktion #Lorentzkraft #Bewegte Ladung #Induktionsspannung #Induktionsstrom

Lorentzkraft

#Induktion #Lorentzkraft #Induktionspannung #Induktionsstrom

Auf ein geladenes Teilchen wirkt im homogenen elektrischen Feld der konstanten Feldstärke E die konstante Feldkraft ${\vec{F}}_{el} = Q \cdot \vec{E}$ , wobei Q die Ladung des Teilchens ist. Die Masse m des Ladungsträgers erfährt nach dem newtonschen Grundgesetz der Mechanik die Beschleunigung
$\begin{array}{l} \vec{a} = \frac{{\vec{F}}_{el}}{m} . \\ Das Einsetzen des Ausdrucks für die Feldkraft ergibt: \\ \vec{a} = \frac{Q \cdot \vec{E}}{m} oder \vec{a} = \frac{Q}{m} \cdot \vec{E} \\ Der Quotient \frac{Q}{m} ist die spezifische Ladung, die bei Elektronen \\ einen Betrag von \frac{e}{m} = 1,759 \cdot 10^{11} \frac{C}{kg} hat . \end{array}$

Diese Bewegung wollen wir im Folgenden genauer untersuchen und unterscheiden dazu, analog zur Kinematik eines Massepunktes, zwei Fälle:

(1)	Die Anfangsgeschwindigkeit des geladenen Teilchens ist parallel zu den Feldlinien des elektrischen Feldes (entspricht dem senkrechten Wurf bzw. dem freien Fall).

(2)	Die Anfangsgeschwindigkeit des geladenen Teilchens ist senkrecht zu den Feldlinien des elektrischen Feldes (entspricht dem waagerechten Wurf).

(1) Anfangsgeschwindigkeit ist parallel zu den Feldlinien

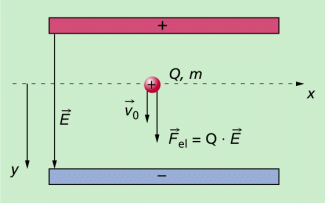
Ein positiv geladenes Teilchen mit der Anfangsgeschwindigkeit $v_{0}$ , der Masse m und der Ladung Q bewege sich parallel zu den Feldlinien eines homogenen elektrischen Feldes, z. B. eines Plattenkondensators (Bild 1).
Entsprechend der Beziehung (1) wird dieser Ladungsträger mit

a = \frac{Q}{m} \cdot E

in Richtung der Feldstärke beschleunigt. Hat die Ladung ein negatives Vorzeichen, so erfährt sie eine Beschleunigung gegen die Feldrichtung.
Da die wirkende Kraft und die Geschwindigkeit gleichgerichtet sind, reicht eine Betrachtung der Beträge aus. Nach der Zeit t hat die Ladung den Weg

y = v_{0} \cdot t + \frac{1}{2} \frac{Q}{m} \cdot E \cdot t^{2}

zurückgelegt. Dies ist das aus der Kinematik bekannte Gesetz der gleichmäßig beschleunigten Bewegung, wobei die Beschleunigung a durch die oben abgeleitete Beschleunigung im konstanten elektrischen Feld ersetzt wurde. Differenzieren der Beziehung nach der Zeit ergibt die Geschwindigkeit zum Zeitpunkt t. Man erhält:

v = \frac{d y}{d t} = v_{0} + \frac{Q}{m} \cdot E \cdot t

In vielen Fällen kann die Anfangsgeschwindigkeit des geladenenTeilchens vernachlässigt werden. Ein Beispiel dafür sind Elektronen, die mit der Austrittsgeschwindigkeit v = 0 von einer Katode emittiert werden. Für die zurückgelegte Strecke gilt dann
$\begin{array}{l} y = \frac{1}{2} \frac{Q}{m} \cdot E \cdot t^{2} \\ und für die Geschwindigkeit \\ v = \frac{Q}{m} \cdot E \cdot t . \end{array}$

Stellt man die zuletzt genannte Gleichung nach der Zeit um und setzt diese Zeit in die Gleichung für den Weg y ein, so erhält man:

$\begin{array}{l} y = \frac{1}{2} \frac{Q}{m} \cdot E \cdot {(\frac{m \cdot v}{Q \cdot E})}^{2} \\ Durch Quadrieren und Kürzen erhält man: \\ y = \frac{1}{2} \frac{m \cdot v^{2}}{Q \cdot E} \\ Umgestellt nach der Geschwindigkeit v ergibt: \\ v = \sqrt{\frac{2 Q \cdot E \cdot y}{m}} \\ Da im homogenen elektrischen Feld das Produkt E \cdot y \\ gleich der Spannung U ist, kann man auch schreiben: \\ v = \sqrt{2 U \cdot \frac{Q}{m}} \\ Für Elektronen lautet die Gleichung dann: \\ v = \sqrt{2 U \cdot \frac{e}{m}} \end{array}$
Die Geschwindigkeit eines geladenen Teilchens hängt also von seiner spezifischen Ladung und von der Spannung ab.

Eine positive Ladung wird in Richtung des elektrischen Feldes beschleunigt.

(2) Anfangsgeschwindigkeit ist senkrecht zu den Feldlinien

Ein geladenes Teilchen wird beim Durchlaufen einer Beschleunigungsspannung gemäß Gleichung der zuletzt abgeleiteten Gleichung auf die Geschwindigkeit

v = \sqrt{2 U_{B} \cdot \frac{Q}{m}}

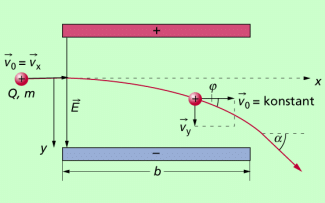
beschleunigt und anschließend senkrecht zu den Feldlinien eines homogenen elektrischen Feldes, wie es z. B. zwischen den Platten eines Plattenkondensators besteht, eingebracht. Unter der Wirkung der elektrischen Kraft vollzieht das Teilchen eine gleichmäßig beschleunigte Bewegung in Feldrichtung, die sich mit der gleichförmigen Bewegung senkrecht zu den Feldlinien überlagert (Bild 2).

Als Bahnkurve entsteht wie beim waagerechten Wurf eine parabelförmige Bahn. Nach dem Gesetz der ungestörten Überlagerung ( Superpositionsprinzip ) setzt sie sich zusammen aus der Bewegung mit konstanter Geschwindigkeit in x-Richtung mit $v_{x} = v_{0}$ und einer gleichmäßig beschleunigten Bewegung in y-Richtung. Die Beschleunigung in dieser Richtung beträgt
$\begin{array}{l} a = \frac{F}{m} = \frac{Q \cdot E}{m}, \\ die Geschwindigkeit in dieser Richtung ist dann \\ v_{y} = a \cdot t = \frac{Q \cdot E}{m} \cdot t . \end{array}$

Für die zurückgelegten Wege zur Zeit t gilt analog zum waagerechten Wurf:

x = v_{0} \cdot t y = \frac{1}{2} \frac{Q \cdot E}{m} t^{2}

Eliminiert man aus den beiden Gleichungen die Zeit, indem man die erste Glecihung nach t auflöst in in die zweite Gleichung einsetzt, so erhält man die Gleichung für die Bahnkurve:

\begin{array}{l} y = \frac{1}{2} \frac{Q \cdot E}{m} {(\frac{x}{v_{0}})}^{2} \\ Durch Umformung erhält man: \\ y = \frac{Q \cdot E}{2 m \cdot v_{0}^{2}} x^{2} \end{array}

Das geladeneTeilchen bewegt sich also auf einer Parabel durch den Kondensator. Da die Gravitationskraft im Vergleich zur Feldkraft vernachlässigbar ist, wurde diese zur Herleitung der Bahnkurve nicht berücksichtigt. Sie kann auch bei Anwendungen vernachlässigt werden.

Als nächstes soll der Austrittswinkel $α$ berechnet werden (Bild 2). Allgemein gilt für die Ablenkung:
$\tan ϕ = \frac{v_{y}}{v_{x}} = \frac{Q \cdot E}{m \cdot v_{0}} t$

Um daraus den Austrittswinkel berechnen zu können, muss in die Gleichung die Zeit eingesetzt werden, die das Teilchen zum Durchqueren des Plattenkondensators benötigt. Sie beträgt:
$t = \frac{b}{v_{0}}$
Zusätzlich kann die elektrische Feldstärke E (sie errechnet sich aus dem Quotienten der anliegenden Spannung U und dem Plattenabstand d) sowie die Anfangsgeschwindigkeit eliminiert werden. Man erhält:
$\tan α = \frac{b \cdot U}{2 d \cdot U_{B}}$
Die Ablenkung eines geladenen Teilchens, das senkrecht zu den Feldlinien eingeschossen wird, ist also proportional zur Länge des Kondensators und proportional zur anliegenden Spannung. Dagegen nimmt die Ablenkung bei zunehmendem Plattenabstand sowie zunehmender Anfangsgeschwindigkeit bzw. Beschleunigungsspannung ab.

Eine elektrische Ladung, die senkrecht zu den Feldlinien eingeschossen wird, bewegt sich auf einer parabelförmigen Bahn im elektrischen Feld.

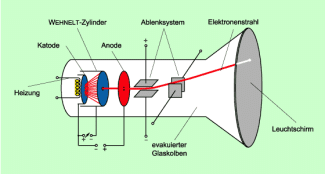
Die Elektronenstrahlröhre - Eine Anwendung im Alltag

Die Elektronenstrahlröhren stellen eine praktische Anwendung der hier dargelegten Theorie da. Sie werden nach ihrem Erfinder, dem deutschen Physiker KARL FERDINAND BRAUN (1850 - 1918), auch braunsche Röhren genannt. Eingesetzt werden sie zur Erzeugung von Bildern, z. B. in Oszillografen. Bei Fernsehbildröhren wird in der Regel eine magnetische Ablenkung genutzt.
Prinzipiell besteht eine Elektronenstrahlröhre aus einem System zur Erzeugung eines Elektronenstrahls, einem Ablenksystem und einem Leuchtschirm (Bild 3). Mit Heizung, Katode, Anode und Wehneltzylinder wird ein Elektronenstrahl erzeugt, der zur Anode beschleunigt wird und sich aufgrund seiner Trägheit durch diese weiterbewegt. Der Wehneltzylinder, benannt nach dem deutschen Physiker ARTHUR WEHNELT (1871-1944), dient dabei der Helligkeitssteuerung. Durch das Ablenksystem wird der Elektronenstrahl horizontal und vertikal so abgelenkt, dass er an einem bestimmten Punkt auf den Leuchtschirm auftrifft. Dort bringt er die Leuchtschicht an der inneren Seite des Schirms zum Leuchten.

Aufbau einer Elektronenstrahlröhre

Physik Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Physik kostenlos lernen

Verwandte Artikel