Beschleunigung

Die Beschleunigung gibt an, wie schnell sich die Geschwindigkeit eines Körpers ändert.

Formelzeichen:	$\vec{a}$
Einheit: ein Meter je Quadratsekunde	$(1 m \cdot s^{- 2})$

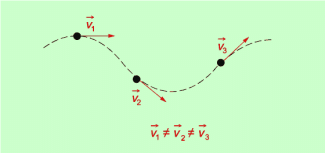
Sie ist eine vektorielle Größe, also ebenso wie Weg und Geschwindigkeit durch Betrag und Richtung bestimmt. Demzufolge liegt eine beschleunigte Bewegung vor, wenn sich bei einer Bewegung

der Betrag der Geschwindigkeit oder
die Richtung der Geschwindigkeit oder
Betrag und Richtung der Geschwindigkeit
ändern.

Spezielle Arten der Beschleunigung sind die bei der Kreisbewegung auftretende Radialbeschleunigung und die beim freien Fall wirkende Fallbeschleunigung.

Beschleunigte Bewegungsabläufe in Diagrammen

#Bewegung #Geschwindigkeit #Beschleunigung #Weg-Zeit-Diagramm

Beschleunigung berechnen

#Bewegung #Geschwindigkeit #Beschleunigung #Weg-Zeit-Diagramm

Ein Beispiel für den ersten Fall ist die Erhöhung der Geschwindigkeit eines Autos längs einer geraden Straße. Fall 2 findet man bei einer gleichförmigen Kreisbewegung, Fall 3 beispielsweise bei einer Person, die in einem anfahrenden Karussell sitzt.

Manchmal wird zwischen Beschleunigung (Betrag der Geschwindigkeit vergrößert sich) und Verzögerung (Betrag der Geschwindigkeit verringert sich) unterschieden. Eine solche Unterscheidung kann auch über eine Vorzeichenvereinbarung erfolgen: Eine positive Beschleunigung bedeutet eine Geschwindigkeitsvergrößerung, eine negative Beschleunigung eine Geschwindigkeitsverringerung. Diese Vorzeichenregelung ergibt sich automatisch aus der in der Physik üblichen Verfahrensweise, bei einer Differenz den Endwert vom Anfangswert zu subtrahieren:
$Δ v = v_{E} - v_{A}$

Beschleunigungen in Natur und Technik

Die Beschleunigung eines Körpers kann sehr unterschiedlich sein. Nachfolgend sind Beispiele für Beschleunigungen angegeben, die in Natur und Technik auftreten.

Vorgang	Beschleunigung in $\frac{m}{s^{2}}$
Tennisball beim Abschlagen	10 000
Auto mit 50 km/h auf ein festes Hindernis	340 ... 540 (je nach Wagentyp)
Schleudersitz bei einem Düsenjäger	140
Düsenjäger beim Kurvenflug	bis 90
Astronaut beim Start einer Rakete	bis 60
Gepard	bis 11
Wegstoßen einer Kugel beim Kugelstoß	ca. 10
fallender Stein	9,81
Auto beim scharfen Bremsen auf trockener Straße	bis 9
Mindestwert beim Bremsen auf trockener Straße (TÜV-Festlegung)	6
Auto beim scharfen Bremsen auf nassem Beton	4
vorsichtige Betriebsbremsung beim PKW	3
mittlere Startbeschleunigung beim Sprint	2,1
Flugzeug (Jumbo-Jet) beim Start	1,6
Zug (ICE) beim Anfahren	0,5
anfahrender Güterzug	0,1

Messen der Beschleunigung

Die Beschleunigung eines Körpers kann mit einem Beschleunigungsmesser gemessen werden. Solche Beschleunigungsmesser zeigen immer die jeweilige Beschleunigung (Augenblicksbeschleunigung oder Momentanbeschleunigung) an.

Berechnen der Beschleunigung

Die Beschleunigung eines Körpers kann berechnet werden mit der Gleichung:
$\begin{array}{l} \vec{a} = \frac{Δ \vec{v}}{Δ t} \\ oder in differenzieller Form \\ \vec{a} = \frac{d \vec{v}}{d t} = \frac{d^{2} s}{d t^{2}} \\ Δ \vec{v}, d \vec{v} Änderung der Geschwindigkeit \\ Δ t Zeitintervall \\ s Weg \end{array}$
Dabei sind folgende Fälle von besonderer Bedeutung:

a)	Die Beschleunigung ist zeitabhängig, ändert sich also zeitlich. Es gilt a = a(t). Dann liegt eine ungleichmäßig beschleunigte Bewegung vor. Um in diesem Falle Aussagen über die Beschleunigung machen zu können, muss man die zeitliche Abhängigkeit der Beschleunigung kennen. Ansonsten kann man aus den Differenzen von Geschwindigkeit und Zeit eine Durchschnittsbeschleunigung berechnen. Das ist z.B. der Fall, wenn man die Beschleunigung eines anfahrenden Autos aus dem Stillstand bis zu einer Geschwindigkeit von 100 km/h ermittelt.
b)	Der Betrag der Beschleunigung ist konstant, also gilt: $a = konstant \neq 0$ Es liegt dann eine gleichmäßig beschleunigte Bewegung vor. Diese Bewegung kann geradlinig oder krummlinig (kreisförmig) sein. In diesem Fall hat die Beschleunigung in jedem Ort der Bewegung den gleichen Betrag.
c)	Ist die Beschleunigung a = 0, so liegt eine unbeschleunigte Bewegung vor.

Für den Fall der gleichmäßig beschleunigten Bewegung gibt es unterschiedliche Möglichkeiten für die Berechnung der Beschleunigung, wobei die jeweiligen Bedingungen zu beachten sind:

Sind die Masse eines Körpers und die auf ihn wirkende beschleunigende (konstante) Kraft bekannt, so kann man die Beschleunigung berechnen mit der Gleichung:
$\begin{array}{l} a = \frac{F}{m} \\ F beschleunigende Kraft \\ m Masse des Körpers \end{array}$

Bewegt sich ein Körper aus der Ruhe heraus gleichmäßig beschleunigt, so kann man die Beschleunigung auch berechnen mit der Gleichungen:
$\begin{array}{l} a = \frac{2 s}{t^{2}} (1) oder a = \frac{v^{2}}{2 s} (2) \\ s Weg \\ v Geschwindigkeit \\ t Zeit \end{array}$
Die Gleichung (1) ergibt sich aus dem Weg-Zeit-Gesetz der gleichmäßig beschleunigten Bewegung durch einfaches Umstellen, die Gleichung (2) aus dem Weg-Zeit-Gesetz und dem Geschwindigkeit-Zeit-Gesetz durch Eliminieren der Zeit t. Die Gleichungen sind auch anwendbar, wenn ein Körper bis zum Stillstand verzögert wird.

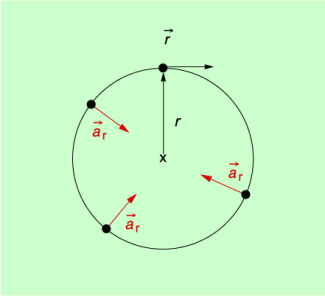
Die Radialbeschleunigung
Für eine gleichförmige Kreisbewegung kann die radial gerichtete Beschleunigung (Bild 3), die als Radialbeschleunigung oder Zentralbeschleunigung oder Zentripetalbeschleunigung bezeichnet wird, berechnet werden mit folgenden Gleichungen:

$\begin{array}{l} a_{r} = \frac{v^{2}}{r} a_{r} = ω^{2} \cdot r a_{r} = \frac{4 π^{2} \cdot r}{T^{2}} \\ a_{r} = 4 π^{2} \cdot n^{2} \cdot r \\ v Bahngeschwindigkeit \\ r Bahnradius \\ ω Winkelgeschwindigkeit \\ n Drehzahl \\ T Umlaufzeit \end{array}$

Herleitung der Radialbeschleunigung
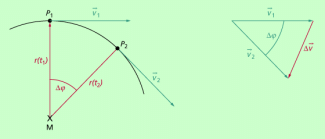
Die Radialbeschleunigung für eine gleichförmige Kreisbewegung kann man folgendermaßen herleiten:
Wir betrachten einen Punkt P, der sich mit konstantem Betrag der Geschwindigkeit auf einer kreisförmigen Bahn bewegt. Bei der Bewegung von
$P_{1} {nach P}_{2}$ wird der Weg s zurückgelegt (Bild 4).
Bei einem kleinen Winkel $\begin{array}{l} Δ φ {ergibt sich aus dem Dreieck MP}_{1} P_{2} für den Weg: \\ Δ s = r \cdot Δ φ (1) \\ Aus dem Dreieck für die Geschwindigkeiten (Bild 4) \\ erhält man: \\ Δ v = v \cdot Δ φ (2) \end{array}$

Stellt man die Gleichungen (1) und (2) nach dem Winkel um und setzt die Terme gleich, so ergibt sich:
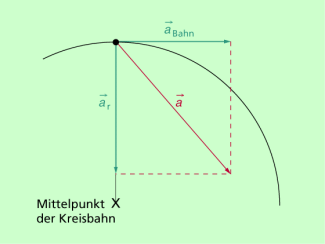
$\begin{array}{l} \frac{Δ s}{r} = \frac{Δ v}{v} oder \\ v \cdot Δ s = r \cdot Δ v \\ Die Division der Gleichung durch Δ t ergibt: \\ v \cdot \frac{Δ s}{Δ t} = r \cdot \frac{Δ v}{Δ t} \\ Der Term \frac{Δ s}{Δ t} ist die Bahngeschwindigkeit v, \\ der Term \frac{Δ v}{Δ t} ist die gesuchte Beschleunigung a_{r} . \\ Setzt man diese Größen ein, so erhält man: \\ v^{2} = r \cdot a_{r} oder \\ a_{r} = \frac{v^{2}}{r} \\ Mit v = ω \cdot r ergibt sich als eine zweite Gleichung für die \\ Radialbeschleunigung: \\ a_{r} = ω^{2} \cdot r \end{array}$

Beschleunigung bei ungleichförmigen Kreisbewegungen
Bei einer ungleichförmigen Kreisbewegung sind zwei verschiedene Beschleunigungen zu unterscheiden: Zum einen ist eine Bahnbeschleunigung vorhanden, die stets tangential zur Bahn wirkt. Darüber hinaus ist die Radialbeschleunigung vorhanden (Bild 5). Die Gesamtbeschleunigung ergibt sich dann als Vektorsumme der beiden Beschleunigungen. Sie ist nicht in Richtung Mittelpunkt der Kreisbahn gerichtet.

Die Fallbeschleunigung
Eine spezielle Beschleunigung ist die Fallbeschleunigung beim freien Fall eines Körpers, die durch die Gravitationswirkung auf diesen Körper zustandekommt und die auf der Erdoberfläche einen Betrag von $9,81 m \cdot s^{- 2} \approx 10 m \cdot s^{- 2}$ hat. Genauere Informationen zur Fallbeschleunigung sind unter diesem Stichwort auf der CD zu finden.

Physik Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Physik kostenlos lernen

Verwandte Artikel