Galileisches Relativitätsprinzip
Das galileische Relativitätsprinzip trifft eine Aussage über die Gleichwertigkeit von verschiedenen Bezugssystemen in der klassischen Physik, also bei Geschwindigkeiten weit unterhalb der Lichtgeschwindigkeit. Es lautet:
Alle Inertialsysteme sind gleichberechtigt. In ihnen gelten die gleichen physikalischen Gesetze.
Daraus lassen sich Gleichungen ableiten, die es ermöglichen, die räumlichen und zeitlichen Koordinaten eines Punktes von einem Intertialsystem in ein anderes umzurechnen (GALILEI-Transformation).
Was bedeutet galileisches Relativitätsprinzip?
Bewegungen von Körpern und Kräfte auf Körper können in unterschiedlichen Bezugssystemen beschrieben werden. Ein solches System kann sich in Ruhe befinden. Es kann sich auch gleichförmig oder beschleunigt bewegen. So kann man z.B. die Bewegung einer Person in der Gondel eines Kettenkarussells von einem mit dem Erdboden verbundenen (ruhenden) Bezugssystem aus beschreiben. In einem solchen Bezugssystem führt die Person eine gleichförmige Kreisbewegung aus. Dabei wirkt eine Kraft in Richtung Zentrum der Drehbewegung, die Radialkraft.
In einem mitrotierenden Bezugssystem ruht die Person. Auf sie wirkt in diesem beschleunigten Bezugssystem eine Kraft nach außen, die Zentrifugalkraft.
Eine spezielle Gruppe von Bezugssystemen sind Inertialsysteme, also solche Systeme, in denen das Trägheitsgesetz gilt. Alle nachfolgenden Aussagen beziehen sich auf solche Inertialsysteme. Daraus ergibt sich auch der Bezug zu G. GALILEI, der als Erster das Trägheitsgesetz formulierte.
Befindet man sich z.B. in einem abgeschlossenen Raum, dann kann man durch einfache physikalisch Experimente nicht entscheiden, ob dieser Raum ruht oder ob er sich geradlinig und gleichförmig in irgendeiner Richtung bewegt. Ein Körper, der an einer Feder hängt, dehnt diese Feder. Ein rollender Ball bewegt sich geradlinig. Lässt man einen schweren Körper los, so fällt er nach unten. Eine Waage, auf die man sich stellt, zeigt einen bestimmten, immer gleichen Wert an. Die verschiedenen Inertialsysteme sind offensichtlich gleichberechtigt. Körper verhalten sich in ihnen in gleicher Art und Weise. Das ist eine grundlegende Aussage für die klassische Physik und wird als galileisches Relativitätsprinzip bezeichnet. Galileisches Relativitätsprinzip bedeutet:
Alle Inertialsysteme sind gleichberechtigt. In ihnen gelten die physikalischen Gesetze in gleicher Art und Weise.
Die GALILEI-Transformation
Aus dem galileischen Relativitätsprinzip folgt, dass es kein bevorzugtes Inertialsystem gibt. Das wiederum heißt aber nicht, dass z.B. die Geschwindigkeit eines Körpers, von zwei verschiedenen Inertialsystemen aus beschrieben, gleich ist. Entsprechendes gilt auch für die Koordinaten eines Körpers.
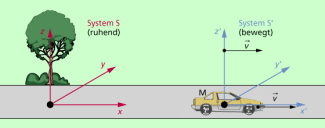
Beispiel: Wir betrachten die Bewegung eines Körpers von zwei verschiedenen Inertialsysteme aus (Bild 2). Das System S soll fest mit der Straße verbunden sein, das System S' ist mit dem fahrenden Auto verbunden und bewegt sich gegenüber dem System S gleichförmig und geradlinig in x-Richtung nach rechts. Dann gilt für die Bewegung des Autos:
- Gegenüber dem System S bewegt sich das Auto mit der Geschwindigkeit v.
- Gegenüber dem System S' befindet sich das Auto in Ruhe.
Auch die Koordinaten des Punktes M (Massemittelpunkt des Autos) sind von den beiden Systemen aus betrachtet unterschiedlich.
Es gibt aber eine relativ einfache Möglichkeit, die Koordinaten in dem einen System in die des anderen Systems umzurechnen.
Die Gleichungen, die es ermöglichen, die räumlichen und zeitlichen Koordinaten eines Punktes von einem Inertialsystem in ein anderes umzurechnen, werden als GALILEI-Transformation bezeichnet.
Dazu gehen wir von den auch in Bild 2 dargestellten Bedingungen aus:
- Wir betrachten die Koordinaten des Massemittelpunktes M des Autos.
- Das System S' bewegt sich gegenüber dem System S mit konstanter Geschwindigkeit v entlang der x-Achse.
- Zum Zeitpunkt t = t' = 0 ist auch x = x' = 0, die Ursprünge der beiden Koordinatensysteme fallen also zu diesem Zeitpunkt zusammen.
Dann ergibt sich als GALILEI-Transformation:
| Umrechnung von S nach S' | Umrechnung von S' nach S |
| y' = y | y = y' |
| z' = z | z = z' |
| t' = t | t = t' |
Bewegen sich die Systeme z.B. entgegen der positiven x-Richtung oder in y-Richtung oder in z-Richtung zueinander, so sind die genannten Tranformationsgleichungen jeweils anzupassen. An ihrer Struktur ändert sich dabei nichts.
Verhalten von Größen bei der GALILEI-Transformation
Bei der Transformation von physikalischen Größen von einem Bezugssystem in ein anderes bleiben einige der Größen unverändert, andere verändern wegen des veränderten Bezugssystems ihren Wert. Größen, die bei der Transformation von einem Bezugssystem ein anderes ihren Wert nicht ändern, bezeichnet man als invariante Größen oder kurz als Invariante.
Eine genauere Prüfung für die GALILEI-Transformation ergibt die in der nachfolgenden Übersicht dargestellten invarianten Größen und diejenigen, deren Wert sich beim Übergang von einem Inertialsystem in ein dazu bewegtes ändern.
| Physikalische Größe | Verhalten des Wertes bei einer Transformation |
| Zeit | invariant |
| Zeitdauer (Zeitintervall) | invariant |
| Länge eines Körpers (Abstand zweier Punkte) | invariant |
| Änderung der Geschwindigkeit | invariant |
| Beschleunigung | invariant |
| Masse | invariant |
| Weg | relativ |
| Geschwindigkeit | relativ |
| Impuls | relativ |
| kinetische Energie | relativ |
-
Betrachtet wird die Bewegung eines Autos zum einen in einem ruhenden System S und zum anderen in einem dazu gleichförmig und geradlinig bewegten System S'.
Wikipedia
Weitere Größen und Gesetze in verschiedenen Inertialsystemen
Mithilfe der GALILEI-Transformation lassen sich auch Gesetze von einem Inertialsystem in ein anderes transformieren. Dabei ist zu beachten, in welcher Richtung diese Transformation erfolgt und welche der Größen invariant bzw. variabel sind.
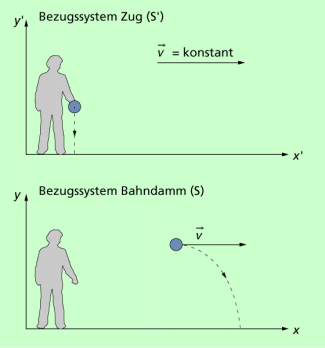
Beispiel: Beschreiben Sie die Bahn eines frei fallenden Körpers in einem bewegten Zug (System S') aus der Sicht eines mitbewegten Beobachters und eines zweiten Beobachters, der am Bahndamm steht (System S)!
Für den mitbewegten Beobachter fällt der Körper senkrecht nach unten. Bei Vernachlässigung der Luftreibung gelten die Gesetze des freien Falls.
Für einen ruhenden Beobachter ist die Bahnkurve eine Parabel, denn der Körper bewegt sich in Fahrtrichtung des Zuges mit der (Anfangs-) Geschwindigkeit v und fällt gleichzeitig nach unten. Wendet man die GALILEI-Transformation auf diesen Körper an, dann ergibt sich für die x-Richtung:
Für die y-Richtung gelten in beiden Systemen die gleichen Gesetze, denn in y-Richtung erfolgt keine Relativbewegung der Systeme zueinander.
-
Die Bahnkurve eines Körpers hängt vom Bezugssystem ab.