Leistung im Wechselstromkreis
Allgemein versteht man unter der elektrischen Leistung den Quotienten aus der an einem Bauelement umgesetzten elektrischen Energie und der Zeit. Im Wechselstromkreis tritt eine Besonderheit auf: An Wirkwiderständen (ohmschen Widerständen) wird elektrische Energie in andere Energieformen umgesetzt. Dagegen „pendelt“ an Blindwiderständen (induktiven und kapazitiven Widerständen) die elektrische Energie zwischen der Quelle und dem Bauelement hin und her, ohne dass die Energie nach außen abgegeben wird. Demzufolge ist analog zu den Wechselstromwiderständen zwischen Wirkleistung P, Blindleistung Q und Scheinleistung S zu unterscheiden. Es gelten folgende Beziehungen:
Die elektrische Leistung
Allgemein versteht man unter der elektrischen Leistung den Quotienten aus der an einem Bauelement umgesetzten elektrischen Energie und der Zeit. Sie lässt sich im Gleichstromkreis berechnen mit der Gleichung:
An Wirkwiderständen (ohmschen Widerständen) wird elektrische Energie in andere, nichtelektrische Energieformen umgesetzt, z.B. in thermische Energie oder in Strahlungsenergie (Licht). Dagegen „pendelt“ an Blindwiderständen (induktiven und kapazitiven Widerständen) die elektrische Energie zwischen der Quelle und dem Bauelement hin und her: Elektrische Energie der Quelle wird in Feldenergie (magnetisches Feld bei der Spule, elektrisches Feld beim Kondensator) umgewandelt und umgekehrt. Dabei wird keine Energie nach außen abgegeben. Demzufolge ist analog zu den Wechselstromwiderständen zwischen Wirkleistung P, Blindleistung Q und Scheinleistung S zu unterscheiden. Dabei ist allerdings zu beachten: Alle Betrachtungen beziehen sich auf den idealisierten Fall reiner ohmscher, induktiver und kapazitiver Widerstände und der Annahme, dass im Stromkreis keinerlei Energieverluste auftreten. Das ist in der Realität nicht der Fall.
Elektrische Leistungen im Wechselstromkreis
Die an ohmschen Widerständen im Wechselstromkreis umgesetzte Leistung wird als Wirkleistung P bezeichnet. Es ist diejenige Leistung, die nach außen abgegeben wird. Sie kann berechnet werden mit der Gleichung:
Sie wird in der Einheit Watt (Kurzzeichen: W) angegeben. Die Blindleistung Q ist die Leistung, die erforderlich ist, um bei den Blindwiderständen (induktiven und kapazitiven Widerständen) kurzzeitig das magnetische bzw. das elektrische Feld aufzubauen. Beim Abbau der Felder wird sie wieder an den Stromkreis abgegeben. Für die Blindleistung Q gilt:
Um die Blindleistung von der Wirkleistung unterscheiden zu können, wird sie in der Elektrotechnik meist in der Einheit Var (Kurzzeichen: var) angegeben. In der Physik wird auch für sie die Einheit Watt genutzt.
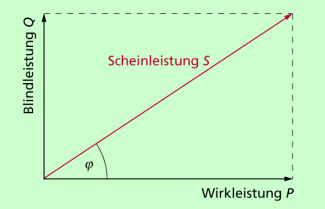
Die Scheinleistung S ist die geometrische Summe aus Wirkleistung und Blindleistung (Bild 1). Für sie gilt:
Um die Scheinleistung von den anderen beiden Leistungen unterscheiden zu können, wird sie in der Elektrotechnik meist in der Einheit Voltampere (Kurzzeichen: VA) angegeben. In der Physik wird auch für sie die Einheit Watt genutzt.
Entscheidenden Einfluss auf die Wirkleistung einer Maschine hat der Leistungsfaktor . Der Winkel ist dabei die Phasenverschiebung zwischen Stromstärke und Spannung. Sie kommt durch induktive und kapazitive Widerstände zustande. Ausführliche Informationen dazu sind unter den betreffenden Stichwörtern zu finden. Besteht keine Phasenverschiebung, so hat der Leistungsfaktor der Wert 1. Die Wirkleistung ist in diesem Fall maximal, die Blindleistung ist null. Je größer die Phasenverschiebung wird, desto kleiner wird die Wirkleistung und desto größer wird die Blindleistung.
Bei elektrischen Maschinen (Motoren, Generatoren, Transformatoren), die alle vorwiegend induktive Widerstände haben, wird im Interesse ihrer Effektivität versucht, durch konstruktive Maßnahmen die Phasenverschiebung möglichst klein zu halten, da die Blindströme die Leitungen der Stromversorgungsnetze zusätzlich belasten. Das erreicht man durch kapazitive Widerstände, die parallel zu den Maschinen mit induktiven Widerständen geschaltet werden. Solche Anordnungen bezeichnet man als Phasenschieberkondensatoren.