Elektrische Arbeit
Die Arbeit zur Bewegung eines solchen Körpers, ist gleich dem Produkt aus seiner Ladung und der Spannung zwischen dem Ausgangs- und dem Endpunkt:
Die am geladenen Körper verrichtete Arbeit ist gleich der Änderung seiner Energie. Für Berechnungen in einem Stromkreis verwendet man eine andere Gleichung. Die Arbeit im elektrischen Stromkreis ist gleich dem Produkt aus Leistung und Zeit, während der die elektrische Leistung aufgewandt wird:
Beide Gleichungen lassen sich ineinander überführen, den
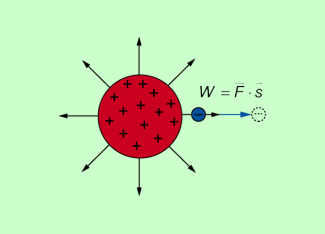
Allgemein gilt: Wendet man eine Kraft F auf, um einen Körper entlang des Weges s zu bewegen, so verrichtet man an diesem Körper Arbeit. Zwei ungleichnamig geladene Körper ziehen sich gegenseitig an. Will man sie auseinanderbringen, so muss man eine Kraft aufbringen, um einen dieser Körper im elektrischen Feld des anderen Körpers zu verschieben. Bei dieser Verschiebung verrichtet man elektrische Arbeit.
Arbeit im elektrischen Feld
Die elektrische Arbeit in einem Plattenkondensator
In einigen Fällen ist die Gleichung für die elektrische Arbeit besonders einfach herzuleiten. Dies ist möglich, wenn die Kraft und der Verschiebungsweg gleich gerichtet sind. Außerdem ist erforderlich, dass die elektrische Feldstärke auf dem gesamten Weg konstant und damit die Kraft ebenfalls konstant ist. Diese Bedingungen sind innerhalb eines Plattenkondensators sehr gut erfüllt. Es soll die elektrische Arbeit berechnet werden, die zu verrichten ist, um einen geladenen Probekörper zwischen zwei Platten eines Plattenkondensators, deren Abstand d beträgt, zu verschieben. Unter den genannten Voraussetzungen gilt für diese Arbeit:
Die Kraft auf einen Probekörper innerhalb eines Plattenkondensator ist das Produkt aus seiner elektrischen Ladung und der elektrischen Feldstärke im Kondensator:
Daraus ergibt sich für die elektrische Arbeit:
Für die elektrische Feldstärke E zwischen den Kondensatorplatten gilt:
(U Spannung zwischen den Platten).
Ersetzt man mithilfe dieser Gleichung die elektrische Feldstärke E in der Berechnungsformel für die elektrische Arbeit, so ergibt sich insgesamt:
Die elektrische Arbeit in einem stromdurchflossenen Leiter
Man darf sich ein gerades Leiterstück wie einen Plattenkondensator mit winzigen Plattenflächen vorstellen. Da an einen Leitungsdraht eine elektrische Spannung angelegt wird und im Leiter elektrische Ladungen fließen - also „verschoben“ werden - verrichtet die Spannungsquelle eine elektrische Arbeit an den Ladungsträgern. Diese Arbeit ist z.B. erforderlich, um den Leitungswiderstand zu überwinden. Da man in einem stromführenden Leiter nicht alle Ladungsträger einzeln „abzählen“ kann, formt man für Arbeitsberechnungen in Stromkreisen die anhand des Plattenkondensators gewonnene Gleichung um.
Die durch ein Leiterstück fließende Gesamtladung ist das Produkt aus Stromstärke I und Zeit:
Für die elektrische Arbeit gilt dann:
Die elektrische Arbeit ist das Produkt aus elektrischer Leistung und Zeit. Diese Gleichung gilt unter der Voraussetzung, dass die im Stromkreis umgesetzte Leistung konstant ist.
Hinweis für Berechnungen der elektrischen Arbeit
Auf elektrischen Bauteilen sind im Regelfall entweder die Leistung oder Spannung und Stromstärke angegeben. So ist beispielsweise jede Glühlampe mit einer Leistungsangabe versehen. Möchte man die elektrische Arbeit einer Glühlampe berechnen, dann muss man diese Leistungsangabe nur noch mit ihrer Betriebsdauer multiplizieren. Eine 100 W-Lampe, die 12 Stunden in Betrieb war, hat demzufolge eine elektrische Arbeit von:
verrichtet.
Material zum Thema
elektrisches Feld Plattenkondensator Elektrische Arbeit Berechnung Stromkreis Kraft elektrische Leistung stromdurchflossener Leiter elektrische Feldstärke Verschiebungsweg Rechenbeispiel
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 