Lösen physikalischer Aufgaben durch Nutzung mathematischer Verfahren und Regeln

Beim Lösen solcher Aufgaben werden physikalische Gesetze in Form von Gleichungen genutzt und mathematische Verfahren und Regeln angewendet. Das betrifft insbesondere Verfahren zum Lösen von Gleichungssystemen, zum Umformen von Gleichungen sowie die Anwendung der Analysis.

Um solche Aufgaben zu lösen, sollte man in folgenden Lösungsschritten vorgehen:

Notieren der für den betreffenden Sachverhalt geltenden Gesetze.
Sind zwei oder mehr Größengleichungen miteinander zu kombinieren, so löst man das Gleichungssystem durch die Substitutions- oder Additionsmethode.
Umformen der Größengleichung nach der gesuchten Größe.
Einsetzen der Werte für die gegebenen Größen und Berechnen der gesuchten Größe. Wenn notwendig, sind vorher Einheiten zweckmäßig umzurechnen.
Beachten der Regeln für das Rechnen mit Näherungswerten bei der Angabe des Ergebnisses.

Arten von Ansätzen

Für das Lösen von mathematischen Aufgaben gibt es in vielen Fällen unterschiedliche Lösungswege. Dabei hat es sich als günstig und rationell erwiesen, zunächst zu prüfen, ob man mit zwei typischen Ansätzen zum Ziel kommt oder ob man einen anderen Lösungsweg suchen muss.

Die beiden typischen Ansätze, mit denen man häufig zu einem Lösungsansatz kommt, sind der energetische Ansatz und der Kraftansatz. Deshalb sollte man beim Herangehen an die Lösung von Aufgaben prüfen:

Ist ein energetischer Ansatz, also die Anwendung des Energieerhaltungssatzes, bei dem gegebenen Sachverhalt möglich?

Beispiel:
Mit welcher Geschwindigkeit trifft eine 65 kg schwere Person auf die Wasseroberfläche auf, wenn sie von einem 5-m-Brett herunterspringt?

Die Aufgabe lässt sich mit einem energetischen Ansatz lösen, wenn man annimmt, dass die gesamt potenzielle Energie der Person, die sie in 5 m Höhe hat, in kinetische Energie umgewandelt wird, also der Energieerhaltungssatz der Mechanik angewendet werden kann. Der Ansatz lautet dann:

$\begin{array}{l} E_{p o t} = E_{k i n} \\ m \cdot g \cdot h = \frac{m}{2} v^{2} \\ Division der Gleichung durch m und Umstellung \\ nach v ergibt: \\ v = \sqrt{2 g \cdot h} \end{array}$

Die Aufgabe lässt sich auch kinematisch lösen, wenn man die Bewegung der Person als freien Fall ohne Anfangsgeschwindigkeit ansieht.
$\begin{array}{l} Aus s = \frac{a}{2} t^{2} und v = a \cdot t erhält man durch Elimieren \\ von t und Umstellen nach v die oben genannte Lösungsgleichung . \end{array}$

Ist ein Kraftansatz möglich?

Beispiel:
Mit welcher maximalen Geschwindigkeit kann ein Auto der Masse m um eine Kurve mit dem Krümmungsradius r fahren, wenn diese Kurve nicht überhöht ist?
Bei einer solchen Kurvenfahrt wird die erforderliche Radialkraft durch die Reibungskraft zwischen Reifen und Straße aufgebracht. Die Maximalgeschwindigkeit ist dann erreicht, wenn die Reibungskraft gerade den Betrag der Radialkraft hat, also gilt:

$\begin{array}{l} F_{radial} = F_{Reibung} \\ m \frac{v^{2}}{r} = μ \cdot m \cdot g \\ v = \sqrt{μ \cdot r \cdot g} \end{array}$

Ist weder ein energetischer Ansatz noch ein Kraftansatz möglich, müssen andere Lösungswege gesucht werden.

Ein weiteres Beispiel

Nachfolgend wird ein weiteres Beispiel ausführlich dargestellt. Dabei wird auch eine Schrittfolge verdeutlicht, die sich bei der Lösung von Aufgaben vielfach bewährt hat und aus den drei Schritten Analyse, Lösung und Ergebnis besteht.

Beispiel
Um Auffahrunfälle zu vermeiden, gibt es für den Abstand von Fahrzeugen folgende Faustregel: Der Abstand von einem Fahrzeug zum nächsten sollte mindestens gleich der Hälfte der Anzeige am Tachometer sein (Geschwindigkeit in km/h, Abstand in m). Wenn ein Auto z. B. mit 80 km/h fährt, sollte der Abstand zum Vordermann mindestens 40 m betragen.

Berechne für einen Pkw mit dieser Geschwindigkeit unter Berücksichtigung der Schrecksekunde den Bremsweg bei einer Vollbremsung, wenn die Bremsverzögerung auf trockener Straße $7 m \cdot s^{- 2}$ beträgt!

Analyse:
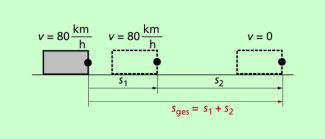
Der Pkw wird als Körper angesehen, der eine verzögerte Bewegung bis zum Stillstand ausführt. Dabei wird eine gleichmäßig verzögerte Bewegung angenommen. Für die Reaktionszeit (Schrecksekunde) kann man eine Sekunde annehmen. In dieser Zeit bewegt sich der Pkw mit der angegebenen Geschwindigkeit von 80 km/h weiter. Der Bremsweg setzt sich demzufolge zusammen aus dem Weg während der gleichförmigen Bewegung in der Schrecksekunde und dem Weg während des Abbremsens bis zum Stillstand (Bild 2).

Gesucht:	$s_{g e s}$
Gegeben:	v = 80 km/h = $80 \cdot \frac{1}{3,6} \frac{m}{s} \approx 22 \frac{m}{s}$
	a = $7 \frac{m}{s^{2}}$
	$t_{1}$ = 1 s

Lösung:
Der Bremsweg ergibt sich als Summe der Wege für beide Bewegungen:

$s_{g e s .} = s_{1} + s_{2}$

Den Weg für die gleichförmige Bewegung während der „Schrecksekunde“ kann man mit dem Weg-Zeit-Gesetz für gleichförmige Bewegungen berechnen:

$s_{1} = v \cdot t_{1}$
$s_{1} =$ $22 \frac{m}{s} \cdot 1 s$
$s_{1} =$ 22 m

Den Weg für die gleichmäßig verzögerte Bewegung kann man nach dem Weg-Zeit-Gesetz für gleichmäßig beschleunigte Bewegungen berechnen:

$s_{2} = \frac{a}{2} t_{2}^{2}$

Da die Zeit $t_{2}$ für diese Bewegung nicht bekannt ist, kann das Geschwindigkeit-Zeit-Gesetz herangezogen werden, denn die Anfangsgeschwindigkeit v ist bekannt. Somit erhält man ein Gleichungssystem aus zwei Gleichungen mit zwei unbekannten Größen ( $s_{2}$ und $t_{2}$ ), das man lösen kann:

$s_{2} = \frac{a}{2} t_{2}^{2}$
	$v = a \cdot t_{2}$
	$↓$
	$t_{2} = \frac{v}{a}$
$s_{2} = \frac{a}{2} (\frac{v^{2}}{a^{2}})$	$↙$
$s_{2} = \frac{v^{2}}{2 a}$

$s_{2} =$ $\frac{s^{2} \cdot 22^{2} m^{2}}{2 \cdot 7 m \cdot s^{2}}$
$s_{2} =$ 35 m

Damit erhält man für den Gesamtweg:

$s_{g e s}$ = 22 m + 35 m
$s_{g e s}$ = 57 m

Ergebnis:
Der Bremsweg bei einer Vollbremsung auf trockener Straße mit einer Anfangsgeschwindigkeit von 80 km/h beträgt unter Berücksichtigung der Schrecksekunde 57 m. Das ist mehr als der Mindestabstand, der nach der Faustregel gefordert wird.

Hinweis: Eine sorgfältige Analyse der Aufgaben zeigt, dass man den Weg 2 auch deutlich einfacher mit einem energetischen Ansatz ermitteln kann. Beim Abbremsen wird kinetische Energie in (negative) Beschleunigungsarbeit umgesetzt. Damit gilt:

$\begin{array}{l} \frac{m}{2} v^{2} = m \cdot a \cdot s_{2} und damit \\ s_{2} = \frac{v^{2}}{2 a} \end{array}$

Der Bremsweg setzt sich aus zwei Teilwegen zusammen.

Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.

Physik Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Physik kostenlos lernen

Verwandte Artikel

Lösen physikalischer Aufgaben durch Nutzung mathematischer Verfahren und Regeln

Arten von Ansätzen

Ein weiteres Beispiel

Rechtliches

Einloggen