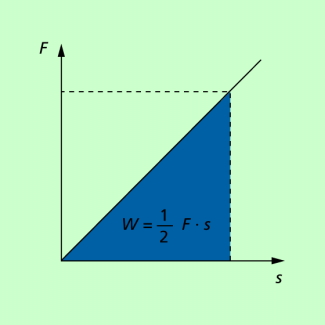Diagramme in der Physik
Zur Veranschaulichung von Zusammenhängen, zur Untersuchung von Verläufen oder zur Darstellung von Abhängigkeiten werden in vielen Bereich von Wissenschaft und Technik Diagramme genutzt. Wichtige Arten von Diagrammen sind Kreisdiagramme, Säulendiagramme (Balkendiagramme) und Liniendiagramme. Eine spezielle Form sind Energieflussdiagramme. Aus Diagrammen lassen sich wichtige Aussagen ableiten. Das ist an Beispielen dargestellt.
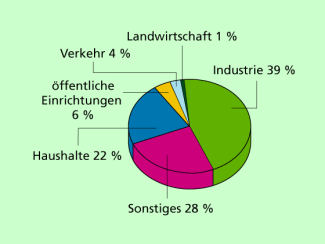
Kreisdiagramme eignen sich besonders dazu, die Anteile von Größen bei einer Ausgangsbasis von 100 % darzustellen. Die prozentualen Anteile werden als Kreissegmente dargestellt. Liegen nur die Prozentzahlen vor, so muss man sie in Winkel umrechnen und dann als Kreissegment abtragen. Dabei gilt:
| 100 % | 360° |
| 1 % | 3,6° |
Zur Anfertigung eines Kreisdiagramms kann natürlich auch ein Computerprogramm genutzt werden.
-
Elektroenergieverbrauch in Deutschland: Dargestellt sind die Anteile einzelner Verbrauchergruppen.
Säulendiagramme oder Balkendiagramme eignen sich besonders dazu, Vergleiche zwischen Größen durchzuführen, wobei 100 % die Ausgangsbasis sein kann, aber nicht sein muss. Die einzelnen Größen werden in Form einer Säule oder eines Balkens dargestellt. Die einzelne Größe wird in Form einer Säule oder eines Balkens dargestellt und kann so anschaulich mit anderen Größen verglichen werden.
-
Primärenergieverbrauch in ausgewählten Ländern je Einwohner und Jahr

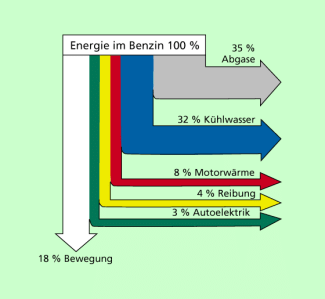
Eine spezielle Form von Säulendiagrammen sind Energieflussdiagramme. In einem solchen Energieflussdiagramm wird dargestellt, wie sich die zugeführte Energie, die mit 100 % angesetzt wird, auf einzelne Bereiche verteilt.
-
Energieflussdiagramm für einen Pkw
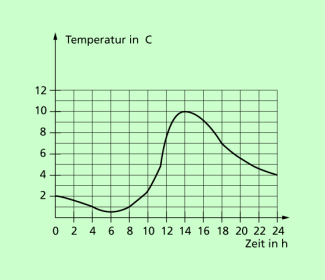
Liniendiagramme (Bild 1) eignen sich besonders dazu, einen Zusammenhang zwischen zwei Größen darzustellen. Aus dem Kurvenverlauf ist ablesbar, wie sich die eine Größe in Abhängigkeit von der anderen Größe ändert.
Interpretation von Liniendiagrammen
Das sinnvolle Interpretieren von Diagrammen ist in vielen Bereichen von Wissenschaft und Technik und damit auch in der Physik eine wichtige Aufgabe. Ausführliche Hinweise zum Interpretieren von Liniendiagrammen sind unter dem Stichwort „Interpretieren“ zu finden.
Bei vielen Liniendiagrammen kann man nicht nur den Zusammenhang zwischen den beiden auf den Achsen abgetragenen Größen erkennen. Manchmal haben auch der Anstieg des Graphen und die Fläche unter dem Graphen eine physikalische Bedeutung.
-
Temperatur-Zeit-Diagramm für einen Tag von 0Uhr bis 24 Uhr
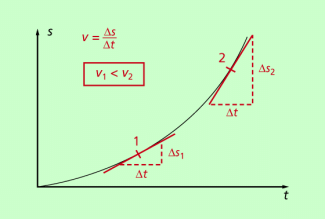
So ist z. B. in einem Weg-Zeit-Diagramm der Anstieg des Graphen gleich der Geschwindigkeit (Bild 2). In einem Geschwindigkeit-Zeit-Diagramm ist der Anstieg gleich der Beschleunigung. Allgemein gilt:
Der Anstieg eines Graphen ist gleich dem Quotienten aus den beiden auf den Achsen abgetragenen Größen. Hat dieser Quotient eine physikalische Bedeutung, so hat der Anstieg des Graphen die gleiche physikalische Bedeutung.
-
s-t-Diagramm: Der Anstieg des Graphen ist gleich der Geschwindigkeit.
Bei einem Kraft-Weg-Diagramm oder bei einem Geschwindigkeit-Zeit-Diagramm hat auch die Fläche unter dem Graphen eine physikalische Bedeutung. Im F-s-Diagramm oder p-V-Diagrammen ist sie gleich der verrichteten mechanischen Arbeit, im v-t-Diagramm ist sie gleich dem zurückgelegten Weg.
Allgemein gilt: Die Fläche unter dem Graphen ist gleich dem Produkt aus den beiden auf den Achsen abgetragenen Größen, manchmal mit einem Faktor ungleich 1 versehen. Hat dieses Produkt eine physikalische Bedeutung, so hat die Fläche unter dem Graphen die gleiche physikalische Bedeutung.
Deshalb ist beim Interpretieren von Liniendiagrammen in der Physik immer zu prüfen, ob man nicht nur aus dem Kurvenverlauf, sondern auch aus dem Anstieg des Graphen oder aus der Fläche unter dem Graphen Aussagen ableiten kann.
-
F-s-Diagramm: Die Fläche unter dem Graphen ist gleich der mechanischen Arbeit.