Weg-Zeit-Diagramme

Für jede Art von Bewegung ergibt sich ein charakteristisches s-t-Diagramm.

Bewegungen mit konstantem Betrag der Geschwindigkeit

Solche Bewegungen mit einem konstanten Betrag der Geschwindigkeit sind die gleichförmige geradlinige Bewegung und die gleichförmige Kreisbewegung. Bei ihnen nimmt der Weg mit der Zeit gleichmäßig zu. Es gilt: $s~t^{}$.
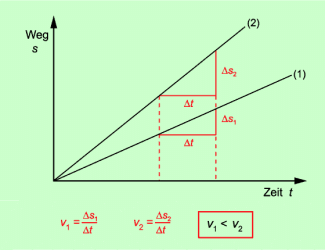
In der grafischen Darstellung ergibt sich als Graph eine Gerade. Je größer die Geschwindigkeit ist, desto steiler verläuft im s-t-Diagramm der Graph (Bild 1). Der Anstieg des Graphen ist gleich der Geschwindigkeit.

Bewegungen mit konstantem Betrag der Beschleunigung längs der Bahn

Solche Bewegungen, bei denen die Beschleunigung längs der Bahn einen konstanten Betrag hat, sind die gleichmäßig beschleunigte geradlinige Bewegung, die gleichmäßig beschleunigte Kreisbewegung und der freie Fall als eine spezielle gleichmäßig beschleunigte geradlinige Bewegung. Bei diesen Bewegungen nimmt der Weg mit dem Quadrat der Zeit zu.
Es gilt: $s~t^2$.
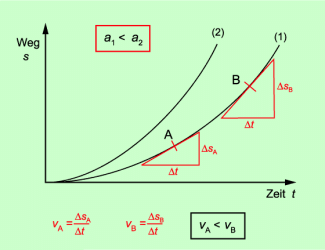
In der grafischen Darstellung ergibt sich als Graph eine Parabel. Je größer die Beschleunigung ist, desto steiler verläuft der Graph (Bild 2). Der jeweilige Anstieg ist auch hier gleich der betreffenden Geschwindigkeit.

Bei ungleichmäßig beschleunigten Bewegungen hängt die Form des Graphen vom Verlauf der Bewegung ab, ist aber weder eine Gerade noch Teil einer Parabel.

Bewegungen mit veränderlichem Betrag der Beschleunigung längs der Bahn

Eine solche Bewegung, bei der sich die Beschleunigung längs der Bahn ändert, nennt man ungleichmäßig beschleunigte Bewegung. Eine solche Bewegung ist charakteristisch für Anfahr- und Bremsvorgänge von Fahrzeugen. Im s-t-Diagramm ergibt sich ein Graph, der weder eine Gerade noch parabelförmig ist, sondern eine beliebige andere Form hat. In Bild 3 ist ein Beispiel dargestellt.
Aus dem Kurvenverlauf kann man erkennen, wie sich die Geschwindigkeit mit der Zeit ändert. Damit ist auch eine Aussage über die Beschleunigung in verschiedenen Etappen der Bewegung möglich.
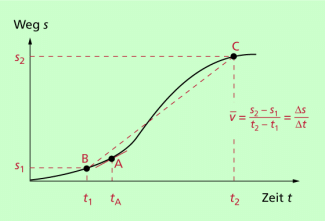
Aus dem Anstieg des Graphen lassen sich Aussagen über die Momentangeschwindigkeit ableiten. Die Momentangeschwindigkeit zu einem bestimmten Zeitpunkt ist gleich dem Anstieg der Tangente an den Graphen zu diesem Zeitpunkt. Das ist in Bild 3 für die Zeit $t_A$ dargestellt.
Der Anstieg der Sekante (gestrichelte Linie zwischen den willkürlich gewählten Punkten B und C in Bild 3) ist gleich der Durchschnittsgeschwindigkeit im Zeitintervall $\Delta t=t_2-t_1$.

Eine notwendige Ergänzung

In der Literatur findet man bezüglich Weg-Zeit-Diagrammen ein unterschiedliches Herangehen:

• Die Graphen in Weg-Zeit-Diagrammen haben immer einen positiven Anstieg oder den Anstieg null, aber nie einen negativen Anstieg (Bild 4).
• Die Graphen in Weg-Zeit-Diagrammen können ansteigen, parallel zur t-Achse verlaufen oder abfallen.

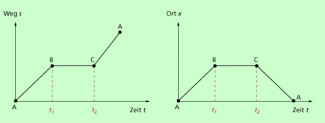
Beide Auffassungen sind möglich, es liegen ihnen aber unterschiedlich Ansatzpunkt zugrunde, die aus Bild 4 erkennbar sind: Wenn man bei den Darstellungen zwischen Weg und Ort differenziert, dann kommt man zu der bei a) dargestellten Variante. Ihr liegt die Auffassung zugrunde, dass sich der zurückgelegte Weg vergrößert, auch wenn man auf irgendeine Weise zum Ausgangspunkt der Bewegung zurückkehrt. Kein Radfahrer würde z.B. behaupten, der von ihm zurückgelegte Weg wäre null, wenn er 20 km von A nach B und anschließend wieder die 20 km von B nach A fährt. In einem Ort-Zeit-Diagramm wäre er aber dann tatsächlich wieder am gleichen Punkt A, nur zu einem anderen Zeitpunkt. In Bild 4 ist das Weg-Zeit-Diagramm und das Ort-Zeit-Diagramm für ein und dieselbe Bewegung dargestellt.

Differenziert man aber nicht zwischen Weg und Ort, dann wird nicht selten die bei b) genannte Variante genutzt. Man meint dann mit dem Weg entweder die längs der Bahn zurückgelegte Strecke oder den Ort. Es gilt: Wenn der Graph fällt, dann kann nur der Ort gemeint sein, auch wenn an der betreffenden Achse Weg steht. Die Punkte B und C repräsentieren den gleichen Ort, den zwischen B und C vergeht zwar eine bestimmte Zeit, es erfolgt aber keine Bewegung.