Kräfte bei der Kreisbewegung

Welche Kräfte bei einer Kreisbewegung wirken, hängt davon ab, welches Bezugssystem man zugrunde legt. Von einem Inertialsystem (unbeschleunigtes, ruhendes Bezugssystem) aus beschrieben gilt:

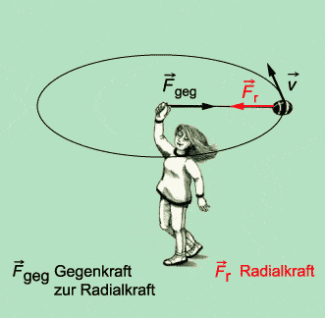
Damit sich ein Körper auf einer Kreisbahn bewegt, muss auf ihn eine Kraft in Richtung Zentrum der Kreisbewegung wirken. Diese Kraft wird als Radialkraft bezeichnet. Sie bewirkt die Radialbeschleunigung und hat den Betrag:

$F_{r} = m \cdot \frac{v^{2}}{r} = m \cdot ω^{2} \cdot r = m \cdot \frac{4 π^{2} \cdot r}{T^{2}} = m \cdot 4 π^{2} \cdot r \cdot n^{2}$

Zu dieser Radialkraft existiert nach dem Wechselwirkungsgesetz eine gleich große, entgegengesetzt gerichtete Gegenkraft, die keine besondere Bezeichnung trägt.
Von einem mitrotierenden (beschleunigten) Bezugssystem aus stellt sich der Sachverhalt anders dar: Auf einen Körper wirkt eine radial nach außen gerichtete Trägheitskraft, die als Zentrifugalkraft bezeichnet wird.

Kim hat in Deutsch, Mathe, Englisch und 6 weiteren Schulfächern immer eine von Lehrkräften geprüfte Erklärung, Video oder Übung parat.
24/7 auf Learnattack.de und WhatsApp mit Bildupload und Sprachnachrichten verfügbar. Ideal, um bei den Hausaufgaben und beim Lernen von Fremdsprachen zu unterstützen.
Viel günstiger als andere Nachhilfe und schützt deine Daten.

Jetzt 30 Tage risikofrei testen

Üblich sind zwei Beschreibungsweisen:

a)	Die Beschreibung erfolgt von einem ruhenden Bezugssystem (Inertialsystem) aus. Ein Beobachter in diesem System beschreibt die Bewegung „von außen“.
b)	Die Beschreibung erfolgt von einem mitbewegten Bezugsystem aus. Da eine Kreisbewegung eine beschleunigte Bewegung ist, führt auch ein mitrotierendes Bezugsystem und ein Beobachter in ihn eine beschleunigte Bewegung aus. Es liegt damit ein beschleunigtes Bezugssystem und kein Inertialsystem vor.

Wir betrachten nachfolgend die Kräfte auf einen Körper, der als Massepunkt angesehen werden kann. Es soll eine gleichförmige Kreisbewegung erfolgen.

Kräfte im ruhenden Bezugssystem
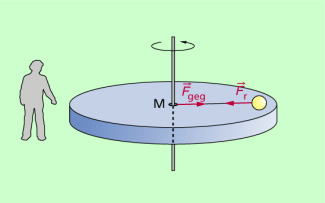
Ein Beobachter betrachtet und beschreibt die Bewegung von außen, so wie das in den Bildern 1 und 2 dargestellt ist. Dann gilt für einen solchen Beobachter:

	Der Körper bewegt sich auf einer Kreisbahn.
	Damit er nicht nach außen wegfliegt, muss eine Kraft in Richtung Zentrum der Bewegung (Kreismittelpunkt) wirken. Diese Kraft wird als Radialkraft, Zentralkraft oder Zentripetalkraft bezeichnet. Der Betrag dieser Kraft kann mithilfe folgender Gleichungen berechnet werden:
$\begin{array}{l} F_{r} = m \cdot \frac{v^{2}}{r} = m \cdot ω^{2} \cdot r = m \cdot \frac{4 π^{2} \cdot r}{T^{2}} = m \cdot 4 π^{2} \cdot r \cdot n^{2} \\ m Masse des Körpers \\ v Geschwindigkeit des Körpers \\ auf der Kreisbahn \\ r Radius der Kreisbahn \\ ω Winkelgeschwindigkeit \\ T Umlaufzeit \\ n Drehzahl \end{array}$
	Die Radialkraft bewirkt eine Radialbeschleunigung oder Zentralbeschleunigung in Richtung Zentrum der Kreisbewegung.
	Als Wechselwirkungskraft wirkt die Gegenkraft zur Radialkraft, die man z.B. bei dem in Bild 1 dargestellten Sachverhalt als Kraft spürt, die an der Hand angreift und nach außen wirkt. Diese Kraft hat den gleichen Betrag wie die Radialkraft, aber die entgegengesetzte Richtung.
	Reißt der Faden, an dem der Körper befestigt ist, so bewegt sich dieser tangential weiter (Beispiel: Hammerwerfen. Beim Loslassen des Hammers fliegt dieser tangential weg.)
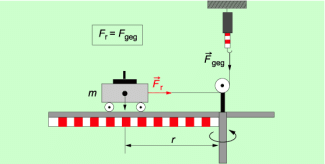
Experimentell kann man die für die Radialkraft geltende Zusammenhänge mit einem Radialkraftmesser bestimmen (Bild 3).


Beispiele für Radialkräfte:
	Bei Satelliten um die Erde oder beim Erdmond ist die Radialkraft die Gravitationskraft, die die Erde auf die betreffenden Himmelskörper ausübt.
	Bei Planeten ist die Radialkraft die Gravitationskraft, die die Sonne auf die Planeten ausübt.
	Bei einem Karussell wird die erforderliche Radialkraft durch die Aufhängung der Gondel aufgebracht.
	Bei Loopingbahnen muss die Bahn selbst die Radialkraft für die Kreisbewegung aufbringen.
	Bei der Ablenkung von Elektronen im homogenen magnetischen Feld ist wirkt die Feldkraft als Radialkraft.

Kräfte im mitbewegten Bezugssystem

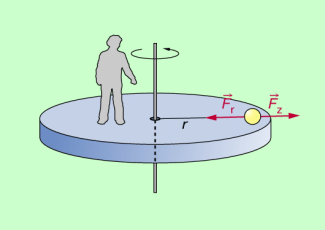
Ein solches mitbewegtes Bezugssystem ist ein bescheunigtes Bezugssystem und damit kein Inertialsystem. Praktisch realisieren kann man das z.B. so, dass ein Beobachter auf einer rotierenden Scheibe steht und von dort aus den Sachverhalt beschreibt (Bild 4). Für einen solchen Beobachter ergibt sich:

	Der Körper befindet sich in Ruhe.
	Auf den Körper wirkt eine nach außen gerichtete Kraft, die man als Zentrifugalkraft oder Fliehkraft bezeichnet. Diese Zentrifugalkraft ist eine Trägheitskraft. Nähere Hinweise zu diesen Kräften sind unter dem betreffenden Stichwort zu finden. Die Zentrifugalkraft hat den gleichen Betrag wie die Radialkraft, kann damit ebenfalls nach den oben genannten Gleichungen berechnet werden.
	Damit der Körper nicht nach außen fliegt, muss eine gleich große Kraft in der entgegengesetzten Richtung wirken. Sie wird z.B. durch einen Faden oder eine Aufhängung aufgebracht.
	Reißt der Faden, an dem der Körper befestigt ist, so bewegt sich dieser tangential weiter.

Zentrifugalkräfte haben in Physik und Technik eine überaus große Bedeutung. So wirken z.B. auf alle Körper, die sich auf der Erdoberfläche befinden, Zentrifugalkräfte, da die Erde um ihre Achse rotiert, wir uns also auf der Erdoberfläche in einem mitbewegten (beschleunigten) Bezugssystem befinden.
Beispiele aus der Technik, bei denen Zentrifugalkräfte genutzt werden, sind Zentrifugen, Kreiselpumpen oder Zentrifugalregler. Gut beobachten kann man diese Kräfte auch bei einem Kettenkarussell. Insbesondere bei schnell rotierenden Anordnungen müssen Zentrifugalkräfte beachtet werden, können sich doch lösende Teile aufgrund der hohen Geschwindigkeiten erhebliche Schäden anrichten.

Lernhelfer (Duden Learnattack GmbH): "Kräfte bei der Kreisbewegung." In: Lernhelfer (Duden Learnattack GmbH). URL: http://www.lernhelfer.de/schuelerlexikon/physik-abitur/artikel/kraefte-bei-der-kreisbewegung (Abgerufen: 19. May 2025, 12:11 UTC)

Suche nach passenden Schlagwörtern

Jetzt durchstarten

Entspannt durch die Schule mit KI-Tutor Kim und Duden Learnattack.

Kim hat in Deutsch, Mathe, Englisch und 6 weiteren Schulfächern immer eine von Lehrkräften geprüfte Erklärung, Video oder Übung parat.
24/7 auf Learnattack.de und WhatsApp mit Bildupload und Sprachnachrichten verfügbar. Ideal, um bei den Hausaufgaben und beim Lernen von Fremdsprachen zu unterstützen.
Viel günstiger als andere Nachhilfe und schützt deine Daten.

Verwandte Artikel

Gewichtskräfte

Die Gewichtskraft gibt an, wie stark ein Körper auf eine Unterlage drückt oder an einer Aufhängung zieht.

Formelzeichen:	${\vec{F}}_{G}$
Einheit:	ein Newton (1 N)

Die Gewichtskraft kann mit der Gleichung ${\vec{F}}_{G} = m \cdot \vec{g}$ berechnet werden. Sie ist wie jede andere Kraft eine gerichtete (vektorielle) Größe. Im Unterschied zur Masse ist die Gewichtskraft vom Ort abhängig, an dem sich der betreffende Körper befindet.
Ein spezieller Fall liegt vor, wenn die Kraft auf eine Unterlage oder eine Aufhängung null ist. Dann spricht man von Schwerelosigkeit oder Gewichtslosigkeit.

Kräfte und ihre Messung

Der Begriff Kraft wird im Alltag und in der Physik in vielfältiger Weise verwendet. Während der Alltagsbegriff mit unterschiedlichen Begriffsinhalten genutzt wird, ist die physikalische Größe Kraft eindeutig definiert:
Die Kraft gibt an, wie stark ein Körper bewegt oder verformt wird. Sie ist eine Wechselwirkungsgröße und eine vektorielle (gerichtete) Größe. Die Wirkung einer Kraft ist abhängig von ihrem Betrag, ihrer Richtung und ihrem Angriffspunkt.

$\begin{array}{l} Formelzeichen: \vec{F} \\ Einheit: ein Newton (1 N) \\ 1 N = 1 \frac{kg \cdot m}{s^{2}} \end{array}$
Man unterscheidet u.a. elektrische Kräfte, magnetische Kräfte, Reibungskräfte, Druckkräfte, Radialkräfte, Gewichtskräfte, Schubkräfte, Spannkräfte und Zugkräfte, Adhäsionskräfte und Kohäsionskräfte, innere Kräfte und äußere Kräfte voneinander.

Fahrphysik

Das Fahrverhalten von Kraftfahrzeugen wird im Wesentlichen durch die Konstruktion (z. B. Vorder-, Hinter- bzw. Allradantrieb, Fahrzeugart, Radstand, Spurweite, Achsbelastung) und das Wirken von äußeren Kräften bestimmt und wird bei besonderen Fahrsituationen (z.B. Anfahren, Bremsen, Kurvenfahrten) deutlich. Dargestellt und an Beispielen erläutert sind die unterschiedlichen Fahrzeugbewegungen, die verschiedenen Arten von Reibung, das Beschleunigen, Bremsen, Kurvenfahrten und Achsbelastungen.

Kurvenfahrten

Zum sicheren Durchfahren einer Kurve muss bei jedem Fahrzeug eine Kraft in Richtung Zentrum der Kreisbewegung wirken. Diese radial gerichtete Kraft, die Radialkraft, wird durch die Reibung zwischen Straße und Reifen aufgebracht.
Die aufzubringende Radialkraft ist umso größer,

je größer die Geschwindigkeit des Fahrzeuges ist,
je größer seine Masse ist,
je kleiner der Krümmungsradius der Kurve ist.

Welche Kräfte bei einer Kurvenfahrt tatsächlich wirken und wie schnell man eine Kurve durchfahren kann, hängt auch davon ab, ob die Kurve überhöht ist und ob man die Bewegung eines vierrädrigen oder eines zweirädrigen Fahrzeuges betrachtet.

Gleichförmige Kreisbewegung

Eine gleichförmige Kreisbewegung liegt vor, wenn sich ein Körper immer mit dem gleichen Betrag der Geschwindigkeit auf einer kreisförmigen Bahn bewegt.
Die gleichförmige Kreisbewegung ist eine beschleunigte Bewegung, da sich ständig die Richtung der Geschwindigkeit ändert.

Kräfte bei der Kreisbewegung

Schule wird easy mit KI-Tutor Kim und Duden Learnattack

Kräfte im mitbewegten Bezugssystem

Suche nach passenden Schlagwörtern