- Lexikon
- Physik Abitur
- 2 Mechanik
- 2.3 Dynamik
- 2.3.3 Arten von Kräften
- Trägheitskräfte
Trägheitskräfte
Das Wesen von Trägheitskräften
Jeder Körper ist träge und schwer. Die Trägheit eines Körpers wirkt immer so, dass er versucht, seinen Bewegungszustand beizubehalten. Für unbeschleunigte Bezugssysteme (Inertialsysteme) wird dieser Sachverhalt mit dem Trägheitsgesetz erfasst, das besagt:
Ein Körper bleibt in Ruhe oder in gleichförmiger, geradliniger Bewegung, solange die Summe der auf ihn wirkenden Kräfte null ist.
Betrachten wir aber die Bewegung eines Körpers in einem beschleunigten Bezugssystem, so stellt sich der Sachverhalt anders dar. Als Beispiel betrachten wir einen anfahrenden Bus und die Kräfte auf eine Person, die in diesem Bus steht (Bild 1).
Aus der Sicht eines ruhenden Beobachters, der am Straßenrand steht, führt der Bus beim Anfahren eine beschleunigte Bewegung aus. Ein Fahrgast wird mit dem Bus zusammen beschleunigt. Für den Zusammenhang zwischen beschleunigender Kraft, Masse des Fahrgastes und seiner Beschleunigung gilt:
Es wirkt also eine Kraft, die eine Beschleunigung bewirkt. Die Gegenkraft wirkt entgegen der Beschleunigungsrichtung. Sie wird z.B. dadurch aufgebracht, dass sich der Fahrgast festhält, um beim Anfahren nicht umzufallen.
Für den Fahrgast im Bus, also im beschleunigten Bezugssystem, stellt sich der Sachverhalt anders dar: Er spürt beim Anfahren eine einzige Kraft, die entgegen der Richtung der Beschleunigung wirkt und ihn nach hinten fallen lässt, wenn er sich nicht festhält (Bild 1). Diese Kraft hat ebenfalls den Betrag . Interpretieren kann man das so: Das Grundgesetz der Mechanik kann man auch in der Form schreiben. Der Term ist dann eine Kraft, die entgegen der beschleunigenden Kraft wirkt und den gleichen Betrag wie sie hat. Das ist genau die Kraft, die ein Fahrgast im beschleunigten Bezugssystem spürt. Allgemein gilt:
In beschleunigten Bezugssystemen wirken Trägheitskräfte. Eine Trägheitskraft wirkt immer entgegengesetzt zur Richtung zur Beschleunigung. Zu einer Trägheitskraft gibt es keine Gegenkraft.
Trägheitskräfte werden mitunter auch als Scheinkräfte bezeichnet. Das ist eine historische Bezeichnung, die nicht darüber hinwegtäuschen darf, dass Trägheitskräfte tatsächlich wirkende Kräfte sind.
Trägheitskräfte bei geradliniger beschleunigter Bewegung
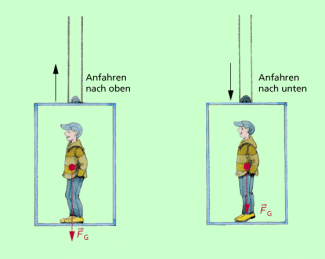
Gut registrieren kann man Trägheitskräfte bei solchen geradlinigen Bewegungen, bei denen man sich z.B. in einem nach oben oder nach unten anfahrenden Fahrstuhl befindet (Bild 2). Beim nach oben anfahrenden Fahrstuhl registriert man eine Trägheitskraft nach unten, die zu der Gewichtskraft (Erdanziehungskraft) hinzukommt und bewirkt, dass sich die nach unten wirkende Kraft vergrößert. Wenn man sich auf eine Personenwaage stellt, dann zeigt diese einen größeren Betrag an. Fährt der Aufzug nach unten an, so verringert sich die auf den Boden wirkende Kraft um die nach oben wirkende Trägheitskraft. Würde der Aufzug gar frei fallen, dann wären Gewichtskraft und nach oben wirkende Trägheitskraft gleich groß. Der Fahrgast wäre schwerelos, würde also keine Kraft auf den Boden des Fahrstuhls ausüben. Wie bereits oben dargestellt, ergibt sich der Betrag der Trägheitskraft aus der Masse des betreffenden Körpers und der Beschleunigung zu:
Trägheitskräfte bei Kreisbewegungen
Sitzt man in der Gondel eines Karussells (Bild 3), dann spürt man eine nach außen wirkende Kraft. Diese auf einen mitrotierenden Beobachter wirkende Kraft ist eine Trägheitskraft und wird bei Kreisbewegungen als Zentrifugalkraft oder Fliehkraft bezeichnet. Nachfolgend sind die Kräfte dargestellt, die in den verschiedenen Bezugssystemen wirken.
Die Zentrifugalkraft hat den gleichen Betrag wie die Radialkraft, aber die entgegengesetzte Richtung. Für den Betrag der Zentrifugalkraft gilt demzufolge:
Trägheitskräfte - Karussell
L. Meyer, Potsdam
Da die Erde um ihre Achse rotiert, ist auch jedes mit der Erdoberfläche verbundenes Bezugssystem ein beschleunigtes Bezugssystem, in dem aufgrund der Erdrotation eine Zentrifugalkraft oder Fliehkraft wirkt. Durch die geringe Winkelgeschwindigkeit der Erde von
ist die auf einen Körper wirkende Zentrifugalkraft so klein, dass sie i.A. vernachlässigt werden kann. Sie ist am Äquator am größten und an den Polen null. Am Äquator beträgt die Zentrifugalkraft ca. 1/200 der Gewichtskraft eines Körpers.
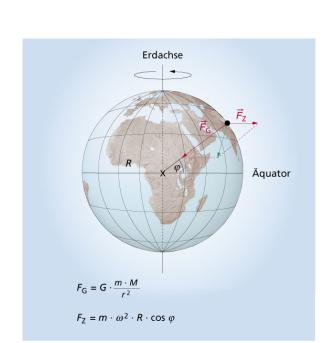
Allgemein wirkt auf einen Körper auf der Erdoberfläche eine von der geografischen Breite abhängige Zentrifugalkraft mit einem Betrag von:
Man beachte: Alle bisherigen Betrachtungen beziehen sich auf eine gleichförmige Rotation der Erde, wobei die Erde als Kugel angesehen wurde. Tatsächlich aber ist sie ein Geoid, sodass bei Messungen Abweichungen von der dargestellten Theorie auftreten.
Zentrifugalkraft und Erdanziehungskraft setzen sich zu einer resultierenden Kraft zusammen (Bild 4). Diese resultierende Kraft messen wir als Gewichtskraft. Das ist auch der physikalische Hintergrund dafür, dass man z.B. manchmal formuliert: Die Gewichtskraft ist näherungsweise die Kraft, mit der ein Körper von der Erde angezogen wird.
Die CORIOLIS-Kraft - eine Trägheitskraft
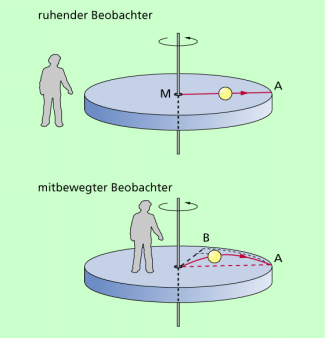
Bewegt sich ein Körper in einem beschleunigten Bezugssystem, so wirkt auf ihn eine zusätzliche Trägheitskraft. Dazu betrachten wir den in Bild 5 dargestellten Fall der Bewegung einer Kugel auf einer sich drehenden Scheibe. Diese Kugel soll im Mittelpunkt der Scheibe einen einmaligen Impuls erhalten.
Für einen ruhenden Beobachter bewegt sich die Kugel auf einer geradlinigen Bahn nach außen (Bild 5, rot eingezeichnete Bahn).
Anders stellt sich der Sachverhalt für einen mitbewegten Beobachter dar. Blickt er zum Zeitpunkt des Beginns der Bewegung der Kugel in Richtung A, so bewegt er sich mit der Scheibe mit und guckt nach der Laufzeit der Kugel auf der Scheibe in Richtung B. Die Bahn der Kugel (rot eingezeichnet) ist für ihn parabelförmig. Erklärbar ist das nur, wenn auf die Kugel eine Querkraft wirkt. Diese Kraft, die auf sich bewegende Körper in einem beschleunigten Bezugssystem wirkt, nennt man CORIOLIS-Kraft, benannt nach dem französischen Physiker und Ingenieur GASPARD GUSTAVE DE CORIOLIS (1792-1843). Die CORIOLIS-Kraft ist wie die Zentrifugalkraft eine Trägheitskraft. Sie kann berechnet werden mit der Gleichung:
Die CORIOLIS-Kraft ist somit stets senkrecht zur Richtung der Geschwindigkeit und zugleich senkrecht zur Winkelgeschwindigkeit gerichtet, die ihrerseits in Richtung Drehachse zeigt. Das bedeutet: Blickt man auf der Nordhalbkugel der Erde in Richtung der Bewegung eines Körpers, so erfolgt durch die CORIOLIS-Kraft eine Ablenkung nach rechts. Das hat z.B. die Konsequenz, dass bei Bewegung von Luft oder Wasser von Süd nach Nord eine Ablenkung in Richtung Osten erfolgt. Das kann man deutlich an Flüssen registrieren, die in dieser Richtung fließen. Für solche Flüsse ist charakteristisch, dass das westliche Ufer häufig flach, das östliche dagegen ein Steilufer ist. Ursache: Durch die langjährige Ablenkung des Wassers in Richtung Osten werden die Ufer solange abgetragen, bis das z.B. durch härtere Gesteinsschichten gebremst wird und sich damit Steilufer bilden.
Ein Angebot von 