- Lexikon
- Physik Abitur
- 2 Mechanik
- 2.2 Kinematik
- 2.2.4 Gleichmäßig beschleunigte geradlinige Bewegungen
- Beschleunigung-Zeit-Diagramme
Beschleunigung-Zeit-Diagramme
Man bezeichnet solche Diagramme als a-t-Diagramme, Beschleunigung-Zeit-Diagramme oder t-a-Diagramme. Welche Variante man bei den Bezeichnungen mit den Kurzzeichen wählt, ist Sache einer Vereinbarung. Wir betrachten darüber hinaus nur die Beschleunigung längs einer Bahn, also die sogenannte Bahnbeschleunigung.
Bewegungen mit konstantem Betrag der Geschwindigkeit längs der Bahn
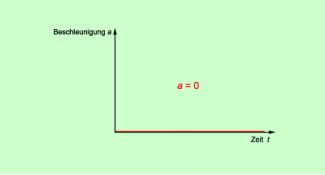
Solche Bewegungen mit einem konstanten Betrag der Geschwindigkeit sind die gleichförmige geradlinige Bewegung und die gleichförmige Kreisbewegung. Bei ihnen bleibt der Betrag der Geschwindigkeit immer gleich. Die Beschleunigung ist null. Es gilt:
v = konstant, a = 0
Damit ergibt sich als Graph eine Gerade, die mit der t-Achse zusammenfällt (Bild 1). Dabei ist bei der gleichförmigen Kreisbewegung zu beachten: Die Bahnbeschleunigung ist null. Sie darf nicht mit der ständig vorhandenen Radialbeschleunigung verwechselt werden.
a-t-Diagramm für eine Bewegung mit der Beschleunigung null (gleichförmige Bewegung)
Bewegungen mit konstantem Betrag der Beschleunigung längs der Bahn
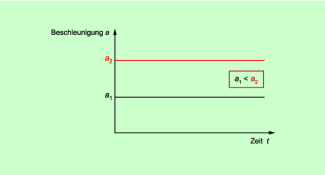
Solche Bewegungen, bei denen die Beschleunigung längs der Bahn einen konstanten Betrag hat, sind die gleichmäßig beschleunigte geradlinige Bewegung, die gleichmäßig beschleunigte Kreisbewegung und der freie Fall als eine spezielle gleichmäßig beschleunigte geradlinige Bewegung. Es gilt:
a = konstant
Der Graph ist eine Gerade, die parallel zur t-Achse verläuft, Je größer die Beschleunigung ist, umso höher liegt der Graph (Bild 2).
a-t-Diagramm für eine Bewegung mit konstantem Betrag der Beschleunigung
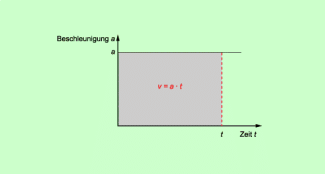
In einem solchen a-t-Diagramm ist die Fläche unter dem Graphen gleich der Geschwindigkeit (Bild 3). Dieser Zusammenhang zwischen der Fläche unter dem Graphen im a-t-Diagramm und der Geschwindigkeit gilt allgemein. Er kann genutzt werden, um bei beliebigen Beschleunigungen über das Auszählen der Fläche die Geschwindigkeit zu ermitteln.
Im a-t-Diagramm ist die Fläche unter dem Graphen gleich der Geschwindigkeit.
Bewegungen mit veränderlichem Betrag der Beschleunigung längs der Bahn
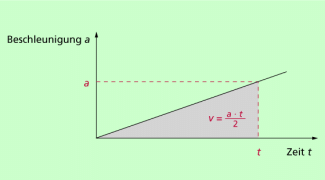
Solche Bewegungen, bei denen die Beschleunigung längs der Bahn nicht konstant ist, werden als ungleichmäßig beschleunigte Bewegungen bezeichnet. Sie treten bei vielen Anfahr- und Bremsvorgängen auf. In Bild 4 ist als Beispiel eine Bewegung dargestellt, bei der die Beschleunigung gleichmäßig zunimmt. Auch in diesem speziellen Fall lässt sich die Geschwindigkeit über die Fläche ermitteln und sogar leicht berechnen. Hat der Graph eine weniger gleichmäßige Form, so kann man aus dem Diagramm durch Auszählen der Fläche die Geschwindigkeit bestimmen.
a-t-Diagramm für eine ungleichmäßig beschleunigte Bewegung
Bahnbeschleunigung a-t-Diagramme gleichmäßig beschleunigte Kreisbewegung ungleichmäßig beschleunigte Bewegungen gleichmäßig beschleunigte geradlinige Bewegung t-a-Diagramme Beschleunigung-Zeit-Diagramme Geschwindigkeit freier Fall Fläche unter dem Graphen gleichförmige Kreisbewegung Graph Gleichförmige geradlinige Bewegung
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 