Gleichmäßig beschleunigte geradlinige Bewegung

Beispiele für solche Bewegungen sind der freie Fall von Körpern, ein mit konstanter Beschleunigung auf gerader Strecke anfahrendes Auto oder ein auf gerader Strecke gleichmäßig abbremsendes Auto. Gleichmäßig beschleunigte Bewegungen können aber auch auf beliebigen anderen Bahnen erfolgen.

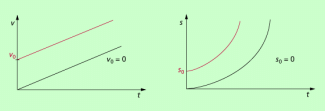
Eine gleichmäßig beschleunigte Bewegung, bei der sich der Körper zum Zeitpunkt t = 0 in Ruhe befindet, lässt sich in verschiedener Weise charakterisieren. Die verschiedenen Möglichkeiten sind in der nachfolgenden Übersicht dargestellt.

Das Weg-Zeit-Gesetz und das Geschwindigeit-Zeit-Gesetz gelten sowohl für geradlinige Bewegungen als auch für krummlinige Bewegungen, wenn die Beschleunigung längs der Bahn einen konstanten Betrag hat.

Gleichmäßig beschleunigter Bewegungen ohne Anfangsweg und Anfangsgeschwindigkeit
Für Berechnungen ist es zweckmäßig, sich die Gesetze für Weg, Geschwindigkeit und Beschleunigung in den unterschiedlichen Formen zusammenzustellen. Die Gleichungen ergeben sich, wenn man aus den beiden Gesetzen
$s=\frac{a}{2}{t}^2\text{und}v=a\cdot t$
entweder a oder t durch Einsetzen in die jeweils andere Gleichung eliminiert.

Beispiel:
$\begin{array}{l}\text{Stellt man die Gleichung}v=a\cdot t\text{nach}a\text{um}\text{,}\\ \text{so erhält man:}\\ a=\frac{v}{t}\\ \text{Setzt man den Ausdruck für}a\text{in die Gleichung}\\ s=\frac{a}{2}{t}^2\text{ein}\text{, so erhält man:}\\ s=\frac{v}{2t}\cdot t^2=\frac{v\cdot t}{2}\\ \text{und damit eine neue Gleichung für den Weg}s\text{,}\\ \text{in der die Beschleunigung}a\text{nicht mehr}\\ \text{vorhanden ist}\text{.}\end{array}$

Gleichmäßig beschleunigter Bewegungen mit Anfangsweg und Anfangsgeschwindigkeit
Viele Bewegungen haben zu dem Zeitpunkt, den man als t = 0 festlegt, bereits eine bestimmte Geschwindigkeit und haben einen bestimmten Weg zurückgelegt. Man spricht dann von einer Bewegung mit Anfangsweg $s_0$ und mit Anfangsgeschwindigkeit $v_0$.
Berücksichtigt man darüber hinaus, dass Weg, Geschwindigkeit und Beschleunigung vektorielle Größen sind und unterschiedliche Richtungen haben können, dann lauten die allgemeinen Gesetze für beliebige gleichmäßig beschleunigte Bewegungen:
$\begin{array}{l}\overrightarrow{s}=\frac{\overrightarrow{a}}{2}{t}^2+{\overrightarrow{v}}_0\cdot t+{\overrightarrow{s}}_0\\ \overrightarrow{v}=\overrightarrow{a}\cdot t+{\overrightarrow{v}}_0\\ \overrightarrow{a}=\text{konstant}\ne 0\end{array}$

Sind die Richtungen von Anfangsweg, Anfangsgeschwindigkeit und Beschleunigung gleich, dann gelten die genannten Gleichungen auch für die Beträge. Entgegengesetzte Richtungen werden durch ein Minuszeichen kenntlich gemacht. So bedeutet z.B. die Gleichung
$v=v_0-a\cdot t:$
Es liegt eine Bewegung mit Anfangsgeschwindigkeit vor, bei der sich die Geschwindigkeit gleichmäßig verringert. Es könnte sich z.B. um ein Auto handeln, das mit einer bestimmten Geschwindigkeit fuhr und ab dem Zeitpunkt t = 0 gleichmäßig abgebremst wird.