Resonanz
Wird ein schwingungsfähiger Körper - wir bezeichnen ihn nachfolgend als Schwinger oder Oszillator - einmalig ausgelenkt und dann sich selbst überlassen, so führt er freie Schwingungen (Eigenschwingungen) mit einer Frequenz aus, die nur von den Eigenschaften des Schwingers abhängt. Diese Frequenz wird als Eigenfrequenz bezeichnet.
Schlägt man z. B. eine Stimmgabel für den Kammerton a an, dann schwingt diese aufgrund ihres Baus mit einer Eigenfrequenz von 440 Hz. Ein einmalig ausgelenktes Fadenpendel schwingt mit einer Eigenfrequenz, die von der Pendellänge abhängt.
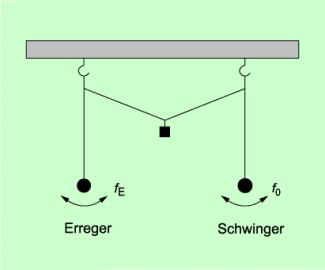
Wird einem Schwinger durch Anregung von außen oder durch Kopplung mit einem zweiten Schwinger Energie zugeführt, so führt er erzwungene Schwingungen aus. Der „Energielieferant“ wird Erreger, seine Frequenz Erregerfrequenz genannt (Bild 1).
Kopplung zweier Fadenpendel. Die Energie wird von einem Pendel zum anderen übertragen.
Liegt die Erregerfrequenz in der Nähe der Eigenfrequenz des Schwingers, so vergrößert sich seine Amplitude. Sie erreicht ein Maximum, wenn die Erregerfrequenz näherungsweise gleich der Eigenfrequenz ist. Dieser Fall wird als Resonanz bezeichnet.
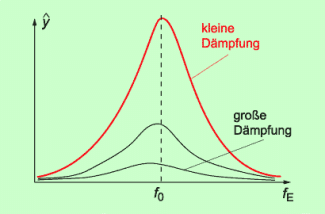
Wie stark sich die Amplitude des Schwingers im Resonanzfall vergrößert, hängt von der Stärke der Dämpfung ab (Bild 2). Bei geringer Dämpfung kann die Amplitude sehr groß werden und es kann sogar zu einer Zerstörung des Schwingers kommen.
Abhängigkeit der Amplitude von der Erregerfrequenz: Die Amplitude ist am größten, wenn die Erregerfrequenz gleich der Eigenfrequenz ist.
Material zum Thema
Erwünschte und unerwünschte Resonanz
Wie viele andere physikalische Erscheinungen ist Resonanz manchmal erwünscht und wird genutzt, manchmal ist sie unerwünscht und muss verhindert werden.
Erwünschte Resonanz finden wir z. B. bei Musikinstrumenten. Viele Musikinstrumente, etwa Gitarren (Bild 3), Geigen, Cellos oder Kontrabässe, verfügen über Resonanzkörper. Diese sind so gebaut, dass bei möglichst vielen Frequenzen ein Mitschwingen erfolgt. Durch den Resonanzkörper wird entscheidend der Klang des betreffenden Instruments bestimmt. Genutzt wird die Resonanz bei Zungenfrequenzmessern. Das sind Messgeräte zur Bestimmung der Frequenz.
Unerwünschte Resonanz dagegen ist das Mitschwingen von Fundamenten bei Maschinen, von Brücken, von Autoteilen oder Fensterscheiben oder das Mitschwingen von hohen Gebäuden oder Türmen. Tritt dort Resonanz auf, so können die Amplituden der Schwingungen so groß werden, dass Schäden oder gar Zerstörungen auftreten. Man spricht dann von einer Resonanzkatastrophe.
Ein klassisches Beispiel für eine solche Katastrophe ist der Einsturz der Tacoma-Hängebrücke in den USA (Bild 4). Diese Ende der dreißiger Jahre des 20. Jahrhunderts gebaute, 1 km lange Hängebrücke stürzte 1940 ein, obwohl zu diesem Zeitpunkt eine relativ geringe Windstärke herrschte.
Durch Windstöße, die zufällig etwa mit der Eigenfrequenz der Brücke erfolgten, schaukelten sich die Schwingungen der Brücke immer mehr auf. Das führte schließlich zum Einsturz. Ein zufällig anwesender Wissenschaftler, der die schon mehrfach beobachteten Schwingungen der Brücke untersuchen wollte, macht mit seiner Schmalfilmkamera sensationelle Aufnahmen von Einsturz der Brücke.
Ein Angebot von 