- Lexikon
- Physik Abitur
- 2 Mechanik
- 2.8 Mechanische Schwingungen und Wellen
- 2.8.1 Entstehung und Beschreibung mechanischer Schwingungen
- Gedämpfte harmonische Schwingungen
Gedämpfte harmonische Schwingungen
Auch bei Fadenpendeln oder Federschwingern zeigt sich dieser Effekt der ständigen Verkleinerung der Amplitude, wenn man sie einmalig anregt und sie dann sich selbst überlässt. Der Vorgang führt letztlich dazu, dass der Schwinger in der Gleichgewichtslage verharrt.
Energieumwandlungen bei mechanischen Schwingungen
Führt ein Schwinger mechanische Schwingungen aus, dann tritt auch immer Reibung auf. Aufgrund von Reibungseffekten wird dann ständig ein Teil der mechanischen Energie, die der Schwinger besitzt, in thermische Energie umgewandelt. Damit verringert sich die mechanische Energie des Schwingers, also auch seine Amplitude (Bild 2). Wie schnell dieser Prozess vor sich geht, hängt von der Stärke der Dämpfung ab. Aus energetischer Sicht gilt für eine gedämpfte Schwingung der Energieerhaltungssatz in der Form:
Die thermische Energie bleibt allerdings nicht im System Schwinger, sondern wird an die Umgebung abgegeben und geht damit dem Schwinger verloren.
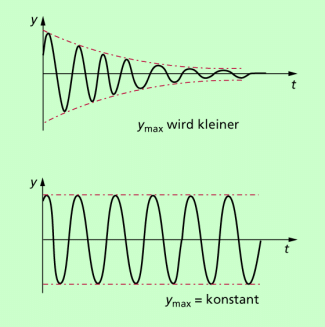
Gedämpfte und ungedämpfte Schwingungen im Vergleich.
Mathematische Beschreibung einer gedämpften harmonischen Schwingung
Eine gedämpfte harmonische Schwingung lässt sich in Form einer Differenzialgleichung erfassen. Sie lautet:
Als Lösung dieser Differenzialgleichung erhält man:
Die Einhüllende der Amplituden wird als Abklingkurve bezeichnet. Wie sie sich in Abhängigkeit vom Abklingkoeffizienten verändert, kann man mit dem nebenstehenden Beispiel selbst ausprobieren. Für den Abklingkoeffizienten können unterschiedliche Werte eingegeben werden. Nach Betätigung der ENTER-Taste erhält man sofort die entsprechende grafische Darstellung.
Aus der Schwingungsgleichung für eine gedämpfte harmonische Schwingung ergibt sich:
- Die maximale Elongation (Amplitude) verringert sich mit der Zeit.
- Die Frequenz der Schwingungen und damit auch die Schwingungsdauer verändert sich mit Verringerung der Amplitude nicht.
Material zum Thema
Ein Angebot von 