Beschreibung mechanischer Schwingungen

Eine mechanische Schwingung kann in unterschiedlicher Weise beschrieben werden. Nachfolgend sind die wichtigsten Möglichkeiten der Beschreibung von Schwingungen dargestellt.

Beschreibung durch Schwingungsaufzeichnung

Der Verlauf von Schwingungen kann in unterschiedlicher Weise aufgezeichnet und damit sichtbar gemacht werden. Die Schwingungen von Stimmgabeln kann man z. B. mit einem Mikrofon empfangen und mit einem Oszillografen sichtbar machen (Bild 1). Eine ähnliche Schwingungskurve erhält man, wenn man eine angeschlagene Stimmgabel mit Schreibspitze über eine berußte Glasplatte zieht.
Die Schwingungen von schweren Fadenpendeln kann man aufzeichnen, wenn man am Pendelkörper in einer Hülse einen senkrecht beweglichen Schreibstift anbringt, die Spitze des Schreibstiftes auf weißes Papier setzt und bei schwingendem Pendel das Papier gleichmäßig wegzieht.

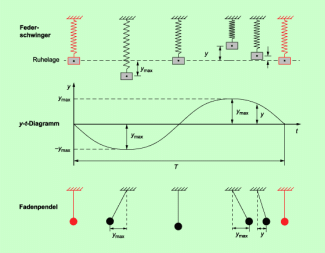
Beschreibung durch ein y-t-Diagramm

Eine Schwingung kann man genauer beschreiben, wenn man den zeitlichen Verlauf der Auslenkung y darstellt. Man erhält dann ein y-t-Diagramm dieser Schwingung (Bild 2). Der Kurvenverlauf entspricht den jeweiligen Schwingungszuständen. In Bild 2 ist in der Mitte ein y-t-Diagramm angegeben. Oben und unten sind die zugehörigen Schwingungszustände für einen Federschwinger und ein Fadenpendel dargestellt.

Beschreibung durch physikalische Größen

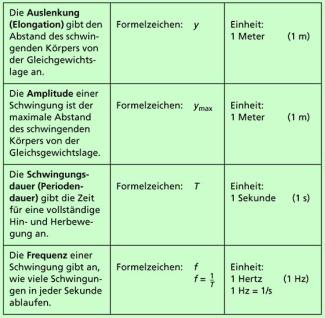
Schwingungen kann man mit den physikalischen Größen Auslenkung (Elongation), Amplitude, Schwingungsdauer (Periodendauer) und Frequenz beschreiben. Diese vier Größen sind in der nachfolgenden Übersicht genauer charakterisiert.

Frequenz und Schwingungsdauer

Frequenz und Schwingungsdauer sind wichtige Größen sowohl für die Beschreibung von mechanischen wie auch von nichtmechanischen Schwingungen. Sie hängen eng miteinander zusammen.
Die Frequenz gibt die Anzahl der schwingungen je Sekunde an. Die Schwingungsdauer, auch Periodendauer genannt, ist die Zeitdauer für eine vollständige Schwingung, also für ein einmaliges Hin- und Herschwingen.
Einheit der Frequenz ist ein Hertz (1 Hz), benannt nach dem deutschen Physiker HEINRICH HERTZ (1857-1894), der die elektromagnetischen Schwingungen und Wellen entdeckt hat.
Vielfache der Einheit 1 Hz sind ein Kilohertz (1 kHz) und ein Megahertz (1 MHz):

Die nachfolgende Übersicht zeigt einige Werte für Frequenzen.

Die Frequenz kann berechnet werden mit den Gleichungen:

$\begin{array}{l}f=\frac{1}{T}\text{und}f=\frac{n}{T}\\ T\text{Schwingungsdauer}\\ n\text{Anzahl der Schwingungen}\\ t\text{Zeit für die n Schwingungen}\\ \text{Durch Umstellung erhält man die entsprechenden}\\ \text{Gleichungen für die Schwingungsdauer:}\\ T=\frac{1}{f}\text{und}T=\frac{t}{n}\text{oder}T=\frac{n}{f}\end{array}$

Beschreibung durch eine Gleichung

Körper können in sehr unterschiedlicher Weise schwingen.
Für harmonische Schwingungen, z. B. die Schwingungen eines Federschwingers oder eines Fadenpendels bei kleinen Auslenkungen, lässt sich eine Schwingungsgleichung angeben, durch die der Verlauf der Schwingung beschrieben wird.
Unter der Bedingung, dass eine harmonische Schwingung vorliegt, gilt:

$\begin{array}{l}y=y_{\max }\cdot \sin (\frac{2\pi }{T}\cdot t)\\ \text{oder}\\ y=y_{\max }\cdot \sin (2\pi \cdot f\cdot t)\\ y\text{Auslenkung (Elongation)}\\ y_{\max }\text{Amplitude}\\ T\text{Schwingungsdauer}\\ t\text{Zeit}\\ f\text{Frequenz}\end{array}$

Der Ausdruck $2\pi \cdot f$ wird auch als Kreisfrequenz $\omega$ bezeichnet. Damit erhält man als Schwingungsgleichung:

$y=y_{\max }\cdot \sin (\omega \cdot t)$

Da harmonische Schwingungen mit einer Sinusfunktion beschrieben werden, spricht man auch von sinusförmigen Schwingungen. Daneben gibt es aber eine Vielzahl von Schwingungen, die nicht sinusförmig verlaufen.

Hat eine harmonische (sinusförmige) Schwingung zum Zeitpunkt t = 0 den Phasenwinkel ${\phi }_0$, dann muss das in der Schwingungsgleichung berücksichtigt werden. Sie lautet dann:

$y=y_{\text{max}}\cdot \sin (\omega \cdot t+{\phi }_0)$

Aus der Schwingungsgleichung lassen sich auch Aussagen über den Verlauf der Geschwindigkeit und der Beschleunigung bei harmonischen Schwingungen ableiten.
Die Geschwindigkeit ergibt sich als erste Ableitung der Elongation nach der Zeit:

$\begin{array}{l}v=\frac{\text{d}y}{\text{d}t}=y_{\text{max}}\cdot \omega \cdot \cos (\omega \cdot t+{\phi }_0)\\ \text{Die maximale Geschwindigkeit wird erreicht}\text{,}\\ \text{wenn der Faktor}\cos (\omega \cdot t+{\phi }_0)=1\text{ist}\text{. Dann}\\ \text{beträgt die Geschwindigkeit:}\\ v=y_{\text{max}}\cdot \omega =y_{\text{max}}\cdot \frac{2\pi }{T}=y_{\text{max}}\cdot 2\pi \cdot f\end{array}$

Diese maximale Geschwindigkeit wird beim Durchgang durch die Gleichgewichtslage erreicht. In den Umkehrpunkten ist sie null.

Die Beschleunigung ergibt sich als erste Ableitung der Geschwindigkeit nach der Zeit bzw. als zweite Ableitung der Elongation:

$\begin{array}{l}a=\frac{\text{d}v}{\text{d}t}=\frac{{\text{d}}^{2}y}{\text{d}{t}^2}=-y_{\max }\cdot {\omega }^2\cdot \sin (\omega \cdot t+{\phi }_0)\\ \text{Setzt man für}{y}_{\max }\cdot \sin (\omega \cdot t+{\phi }_0)=y\text{ein}\text{,}\\ \text{so erhält man:}\\ a=-y\cdot {\omega }^2\\ \text{Die maximale Beschleunigung ergibt sich}\\ \text{für}\sin (\omega \cdot t+{\phi }_0)=1\text{zu:}\\ a=-y_{\max }\cdot {\omega }^2\end{array}$

Die maximale Beschleunigung wird in den Umkehrpunkten erreicht. Beim Durchgang durch die Gleichgewichtslage ist sie null.

Energie bei harmonischen Schwingungen

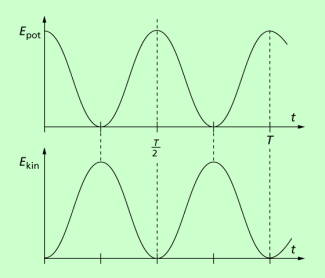
Geht man von einer ungedämpften harmonischen Schwingung aus, dann ändert sich bei mechanischen Schwingern ständig die potenzielle und die kinetische Energie, wobei die Gesamtenergie gleich bleibt (Bild 4).
Daher kann man die Energie eines harmonischen Oszillators z.B. aus seiner maximalen Geschwindigkeit berechnen, weil zum Zeitpunkt der maximalen Geschwindigkeit die kinetische Energie maximal und die potenzielle Energie null sind. Damit erhält man:

$\begin{array}{l}E=E_{\text{kin}\text{,}\max }=\frac{1}{2}m\cdot v^2\text{und mit}v=v_{\max }=y_{\max }\cdot \omega :\\ E=\frac{1}{2}m\cdot y_{\max }^2\cdot {\omega }^2\end{array}$

Bei einem Federschwinger kann man die Energie des Schwingers auch mithilfe der Federkonstanten (Richtgröße, Rückstellfaktor) ausdrücken und erhält dann für die Energie den Ausdruck:

$E=\frac{1}{2}D\cdot y_{\max }^2$

Kraftgesetz für harmonische Schwingungen

Bei einer harmonischen mechanischen Schwingung ist die rücktreibende Kraft proportional zur Auslenkung. Es gilt stets:

$\overrightarrow{F}\sim -\overrightarrow{y}$

Durch das Minuszeichen wird die entgegengesetzte Richtung von Auslenkung und Kraft zum Ausdruck gebracht. Die Kraft wirkt stets entgegen der Auslenkung in Richtung Gleichgewichtslage.
Es gilt auch die umgekehrte Aussage: Besteht zwischen rücktreibender Kraft und Auslenkung bei einem Vorgang Proportionalität, so liegt eine harmonische Schwingung vor. Die Proportionalität zwischen rücktreibender Kraft und Auslenkung ist somit ein Kriterium dafür, ob eine harmonische Schwingung vorliegt oder nicht.

Das Kraftgesetz lässt sich folgendermaßen ableiten:
$\begin{array}{l}\text{Aus dem newtonschen Grundgesetz}\overrightarrow{F}=m\cdot \overrightarrow{a}\\ \text{ergibt sich mit der Beschleunigung}\overrightarrow{a}=-y\cdot {\omega }^2:\\ \overrightarrow{F}=-m\cdot y\cdot {\omega }^2\text{oder}\overrightarrow{F}=-m\cdot {\omega }^2\cdot y.\\ \text{Setzt man den Term}m\cdot {\omega }^2=D,\text{so erhält man:}\\ \overrightarrow{F}=-D\cdot \overrightarrow{y}\end{array}$

Dieses Gesetz wird als Kraftgesetz für harmonische Schwingungen bezeichnet. Den Faktor D nennt man Richtgröße, Rückstellfaktor oder bei Federn auch Federkonstante. Die Gleichung ermöglicht auch die Bestimmung dieser Richtgröße durch Messung von Kraft F und zugehöriger Auslenkung y.