- Lexikon
- Physik Abitur
- 2 Mechanik
- 2.8 Mechanische Schwingungen und Wellen
- 2.8.1 Entstehung und Beschreibung mechanischer Schwingungen
- Mechanische Schwingungen im Überblick
Mechanische Schwingungen im Überblick
Mechanische Schwingungen im Überblick
Kennzeichnung mechanischer Schwingungen
Bei einer Reihe von periodischen Vorgängen bewegt sich ein Körper um eine Gleichgewichtslage (Ruhelage, Nulllage) hin und her. Beispiele dafür sind schwingende Saiten, die Schwingungen einer Stimmgabel (Bild 1) oder eines Pkw auf unebener Fahrbahn, eine Schaukel, ein schwingendes Fadenpendel oder ein Federschwinger. Eine solche spezielle periodische Bewegung bezeichnet man als Schwingung und definiert:
Eine mechanische Schwingung ist eine zeitlich periodische Bewegung eines Körpers um eine Gleichgewichtslage.
Da sich bei mechanischen Schwingungen zeitlich periodisch z.B. der Abstand von der Gleichgewichtslage, die Geschwindigkeit oder die Beschleunigung des betreffenden Körpers ändern, kann man eine Schwingung auch allgemeiner charakterisieren:
Eine Schwingung ist eine zeitlich periodische Änderung physikalischer Größen.
Schwingende Stimmgabel
Mechanische Schwingungen im Überblick - Stimmgabel
L. Meyer, Potsdam
Voraussetzungen für das Zustandekommen mechanischer Schwingungen
Damit überhaupt eine mechanische Schwingung entsteht, müssen folgende Voraussetzungen erfüllt sein:
- Es müssen schwingungsfähige Körper oder Teilchen vorhanden sein. Sie werden auch als Schwinger oder Oszillatoren bezeichnet.
- Die schwingungsfähigen Körper bzw. Teilchen müssen aus ihrer Gleichgewichtslage ausgelenkt werden. Dabei wird in der Regel Energie zugeführt.
- Es muss eine rücktreibende Kraft vorhanden sein, die bewirkt, dass sich der Körper bzw. die Teilchen nach der Auslenkung wieder in Richtung Gleichgewichtslage bewegen.
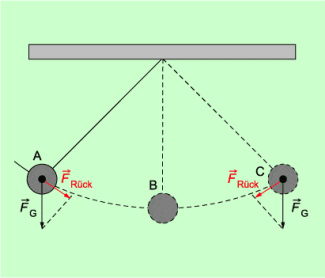
In Bild 2 ist als Beispiel ein Fadenpendel dargestellt. Die rücktreibende Kraft ist in diesem Fall eine Komponente der Gewichtskraft. Sie bewirkt, dass sich der Körper vom Punkt A aus in Richtung Gleichgewichtslage (Punkt B) bewegt und wirkt solange, bis der Körper die Gleichgewichtslage erreicht hat. Aufgrund seiner Trägheit bewegt sich der Körper über die Gleichgewichtslage hinweg bis zum Punkt C. Dabei bewirkt die Gewichtskraft zunächst eine Verlangsamung der Bewegung bis zur Geschwindigkeit null (Punkt C) und anschließend wieder eine Bewegung in Richtung Gleichgewichtslage.
Bei dieser Bewegung ändert sich z. B. die Geschwindigkeit des Körpers: Sie ist in den Punkt A und C (Bild 3) null und hat im Punkt B ihren maximalen Betrag. Es ändert sich auch die Beschleunigung oder die potenzielle Energie. Letztere ist in den Punkten A und C maximal, in Punkt B null. Demgegenüber ist die kinetische Energie in den Punkten A und C null und hat in Punkt B ihren maximalen Wert.
Kräfte bei einem Fadenpendel: Die rücktreibende Kraft ist eine Komponente der Gewichtskraft.
Arten mechanischer Schwingungen
Mechanische Schwingungen können nach der Art der Energiezufuhr und nach der Form der Schwingungen unterschieden werden.
Nach der Art der Energiezufuhr unterscheidet man zwischen freien und erzwungenen Schwingungen. Nach der Form der Schwingungen differenziert man zwischen
- harmonischen und nicht harmonischen Schwingungen sowie
- ungedämpften und gedämpften Schwingungen.
Freie und erzwungene Schwingungen
Körper, die einmalig aus der Ruhelage ausgelenkt werden und sich dann selbst überlassen bleiben, führen freie Schwingungen oder Eigenschwingungen aus. Solche freien Schwingungen führt zum Beispiel eine Stimmgabel aus, die einmal angeschlagen wird und dann schwingt. Das gilt auch für Saiten von Musikinstrumenten, die einmalig angeregt werden. Die Frequenz, mit der ein solcher sich selbst überlassener Körper schwingt, hängt nur von seinen Eigenschaften ab und wird als Eigenfrequenz dieses Schwingers bezeichnet.
Wird dagegen einem schwingenden Körper ständig von außen Energie zugeführt, so führt er erzwungene Schwingungen aus. Das gilt z. B. für ein Kind auf einer Schaukel, das periodisch von außen angestoßen wird. Auch einem Metronom (Bild 3) wird ständig über eine Antriebsfeder Energie zugeführt. Es führt damit erzwungene Schwingungen aus. Eine Maschine kann das Fundament, auf dem sie steht, zu erzwungenen Schwingungen anregen. Und selbst der Wind ist in der Lage, hohe Bauwerke, Bäume oder Brücken zu erzwungenen Schwingungen anzuregen. Erzwungene Schwingungen erfolgen mit der Erregerfrequenz.
Harmonische und nicht harmonische Schwingungen
Nach der Form der Schwingungen kann man zwischen harmonischen und nicht harmonischen Schwingungen unterscheiden.
Harmonische Schwingungen sind dadurch gekennzeichnet, dass man sie mathematisch leicht mithilfe der Sinusfunktion beschreiben kann. Sie werden deshalb auch als sinusförmige Schwingungen bezeichnet. Die Schwingungsgleichung für harmonische Schwingungen lautet:
Material zum Thema
Ungedämpfte und gedämpfte Schwingungen
Nach der Form der Schwingungen kann man zwischen ungedämpften Schwingungen und gedämpfte Schwingungen unterscheiden.
Ein sich selbst überlassener Körper führt immer gedämpfte Schwingungen aus, da stets Reibung auftritt und durch Reibung ein Teil der mechanischen Energie in thermische Energie umgewandelt und als Wärme an die Umgebung abgegeben wird.
Soll ein Körper ungedämpfte Schwingungen ausführen, so muss ihm die Energie, die durch Reibung in thermische Energie umgewandelt wird, periodisch wieder zugeführt werden. Das geschieht z. B. bei einem Uhrpendel durch ein „Uhrengewicht“ und bei einem Metronom durch eine Spiralfeder, die von Zeit zu Zeit aufgezogen werden muss.
Bei gedämpften Schwingungen ist zu beachten, dass sich zwar im Laufe der Zeit die Amplitude verkleinert, die Schwingungszeit und damit auch die Frequenz dabei aber gleich bleibt.
nichtharmonische Schwingungen Erregerfrequenz Berechnung erzwungene Schwingungen mechanische Schwingungen Schwingungsgleichung Trägheit thermische Energie sinusförmige Schwingungen Nulllage ungedämpfte Schwingungen gedämpfte Schwingungen Schwinger freie Schwingungen Gleichgewichtslage periodische Bewegung Reibung harmonische Schwingungen Eigenfrequenz Eigenschwingungen Sinusschwingungen Ruhelage Oszillatoren Rechenbeispiel mechanische Energie
Ein Angebot von 