- Lexikon
- Physik Abitur
- 2 Mechanik
- 2.8 Mechanische Schwingungen und Wellen
- 2.8.2 Überlagerung von Schwingungen
- Überlagerung von Schwingungen
Überlagerung von Schwingungen
Statt von Überlagerung spricht man auch von Superposition.
Überlagerung harmonischer Schwingungen gleicher Frequenz und gleicher Schwingungsrichtung
Wir betrachten zunächst die Überlagerung von zwei harmonischen, also sinusförmigen Schwingungen,
- die die gleiche Frequenz und damit die gleiche Schwingungsdauer haben und
- bei denen die Oszillatoren in der gleichen Richtung hin- und herschwingen.
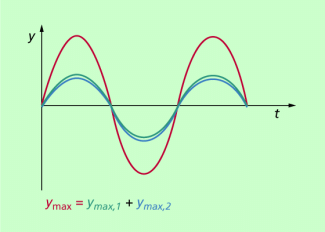
Das Ergebnis der Überlagerung hängt dann von den Amplituden der Einzelschwingungen und von ihrer Phasenlage zueinander ab. In Bild 1 ist der Spezialfall zweier Teilschwingungen gleicher Amplitude dargestellt, wobei die Phasendifferenz zwischen den beiden Schwingungen null ist. Allgemein gilt:
Die resultierende Schwingung ergibt sich durch algebraische Addition der Einzelschwingungen, wobei die Vorzeichen zu beachten sind.
Überlagern sich zwei Schwingungen gleicher Phasenlage und gleicher Amplitude, dann entsteht als resultierende Schwingung eine mit der doppelten Amplitude.
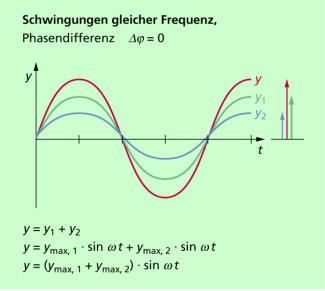
Beträgt die Phasendifferenz zwischen den beiden Teilschwingungen null (Bild 2), dann addieren sich die Auslenkungen an jeder Stelle. Die resultierende Schwingung hat die gleiche Phasenlage, ihre Amplitude ist gleich der Summe der Amplituden der Einzelschwingungen. Es gilt:
Das kann man auch sofort aus dem rechts in Bild 2 gezeichneten Zeigerdiagramm ermitteln.
Überlagerung zweier harmonischer Schwingungen bei einer Phasendifferenz von null. Rechts ist für die im Diagramm markierte Stelle das Zeigerdiagramm dargestellt.
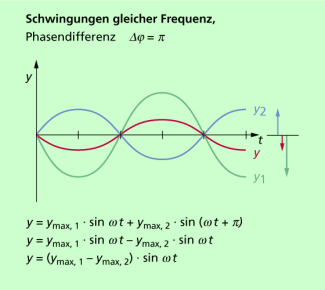
Beträgt die Phasendifferenz zwischen den beiden Teilschwingungen 180° in Gradmaß oder in Bogenmaß (Bild 3), dann ergibt sich aufgrund der Vorzeichen die jeweilige Elongation als Differenz der Elongationen der beiden Teilschwingungen. die Schwingungsgleichung der resultierenden Schwingung lautet:
Auch diese Beziehung kann man sofort aus dem rechts in Bild 3 gezeichneten Zeigerdiagramm ablesen.
Überlagerung zweier harmonischer Schwingungen bei einer Phasendifferenz von 180°. Rechts ist für die im Diagramm markierte Stelle das Zeigerdiagramm dargestellt.
Bei einer beliebigen Phasendifferenz zwischen den beiden Teilschwingungen gibt es drei Möglichkeiten, zu der resultierenden Schwingung zu kommen:
- Es werden im y-t-Diagramm punktweise die Elongationen addiert. Damit erhält man die Schwingungskurve der resultierenden Schwingung, so wie sie in Bild 4 rechts dargestellt ist.
- Man zeichnet für einen bestimmten Zeitpunkt die Zeiger der beiden Einzelschwingungen und addiert diese Zeiger vektoriell (Bild 4 links). Damit kennt man nicht nur die Amplitude der resultierenden Schwingung, sondern auch ihre Phasenlage bezüglich der beiden Einzelschwingungen. Das ist sicher die eleganteste Methode.
- Man arbeitet mit den Schwingungsgleichungen:
Überlagerung zweier harmonischer Schwingungen bei einer beliebigen Phasendifferenz. Aus dem Zeigerdiagramm kann sehr elegant der Zeiger der resultierenden Schwingung ermittelt werden.
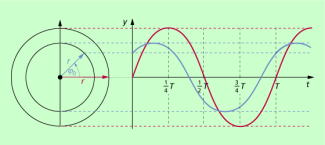
Überlagerung harmonischer Schwingungen unterschiedlicher Frequenz und gleicher Schwingungsrichtung
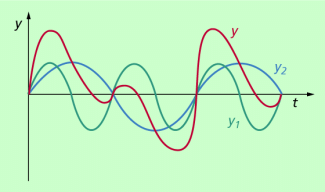
In diesem Fall kommt man nur durch die punktweise Addition der Elongationen zu der resultierenden Schwingung, die in Abhängigkeit von den Frequenzen der Einzelschwingungen und deren Amplituden sehr unterschiedliche Formen haben kann. In Bild 5 ist ein Beispiel dargestellt.
Unterscheiden sich die Frequenzen der beiden Schwingungen, die sich überlagern, nur geringfügig, so entsteht als Resultierende eine Schwingung, deren Frequenz gleich der Differenz aus den Frequenzen der beiden Einzelschwingungen ist. Das bezeichnet man als eine Schwebung. Sie äußert sich z.B. bei Schallschwingungen so, dass man bei zwei Stimmgabeln mit geringen Frequenzunterschieden einen langsam an- und abschwellenden Ton registriert. Beträgt z.B. die Frequenz der einen Teilschwingung 30 Hz und die der anderen 31 Hz, so ist die Frequenz der resultierenden Schwingung
31 Hz - 30 Hz = 1 Hz.
Bei der Überlagerung zweier harmonischer Schwingungen unterschiedlicher Frequenz entsteht eine nicht harmonische Schwingung.
Überlagerung harmonischer Schwingungen bei senkrechter Schwingungsrichtung der Teilchen zueinander
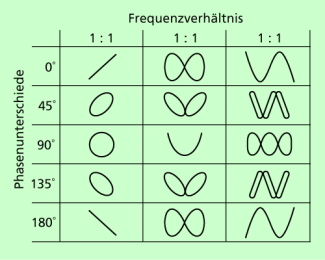
Liegen die Schwingungsrichtung von zwei Teilschwingungen senkrecht zueinander, so findet man die resultierende Schwingung durch vektorielle Addition. Dabei entstehen je nach den Frequenz- und Phasenverhältnissen interessante geometrische Figuren (Bild 6), die nach dem französischen Physik JULES ANTOINE LISSAJOUS (1822-1880) als LISSAJOUS-Figuren bezeichnet werden. Realisieren kann man solche LISSAJOUS-Figuren mithilfe eines Doppelpendels oder mit einem Oszillografen, indem man den einen Generator an die X-Ablenkung und den anderen an die Y-Ablenkung anschließt.
Überlagerung harmonischer Schwingungen unterschiedlicher Schwingungsrichtung (LISSAJOUS-Figuren)
Auslenkung Überlagerung von Schwingungen Superposition resultierende Schwingung Einzelschwingungen Schwingungsgleichung Phasendifferenz Amplitude LISSAJOUS-Figuren Schwebung Phasenlage Elongation Frequenz Simulation Schwingungsdauer
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 