Schwingende Flüssigkeitssäulen und schwimmende Körper

Harmonische mechanische Schwingungen werden nicht nur von Federschwingern und Fadenpendel durchgeführt. Lässt man eine Flüssigkeitssäule in einem U-förmigen Rohr hin- und herschwingen, so führt diese Flüssigkeitssäule ebenfalls harmonische Schwingungen aus, wobei die Schwingungsdauer nur vom Rohrdurchmesser und vom Volumen der eingefüllten Flüssigkeit abhängig ist.
Auch ein Körper, der in einer Flüssigkeit schwimmt, kann eine harmonische Schwingung ausführen, wobei die Schwingungsdauer in diesem Falle von den Dichten des Körpers und der Flüssigkeit sowie von den Abmessungen des Körpers abhängig ist.

Wir betrachten nachfolgend beide Beispiel genauer und leiten Gleichungen für die Schwingungsdauer ab.

Schwingungen einer Flüssigkeitssäule

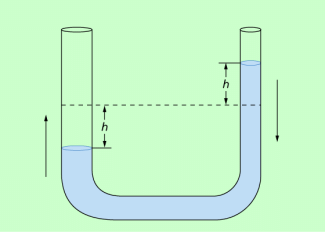
In einem U-Rohr befindet sich eine Flüssigkeit. Ist dieses Rohr waagerecht angeordnet, so steht die Flüssigkeitssäule in beiden Rohren gleich hoch, denn es handelt sich um verbundene Gefäße. Wird die Flüssigkeitssäule ausgelenkt (Bild 1) und dann sich selbst überlassen, so schwingt die Flüssigkeitssäule in dem U-Rohr hin und her. Man spricht dann von Schwingungen einer Flüssigkeitssäule.
Diese Schwingungen sind harmonisch. Eine harmonische Schwingung liegt dann vor, wenn die rücktreibende Kraft proportional zur Auslenkung ist.
Für die rücktreibende Kraft gilt:

F = − p ⋅ A , wobei p der Druck und A die Querschnittsfläche des U-Rohres sind . Mit p = ρ ⋅ g ⋅ 2   h und A = π ⋅ d 2 4 erhält man: F = − ( 1 2   ρ ⋅ g ⋅ π ⋅ d 2 )   h Da für eine bestimmte Flüssigkeit und ein gegebenes U-Rohr die Größen ρ und d und damit auch der gesamte Term in der Klammer konstant sind , ist F ∼ h . Es liegt folglich eine harmonische Schwingung vor .

Für die Schwingungsdauer einer harmonischen Schwingung gilt:
T = 2 π   m D
Die Richtgröße D ergibt sich aus den Betrachtungen zur rücktreibenden Kraft zu:
D = 1 2   ρ ⋅ g ⋅ π ⋅ d 2 (1) Für die Masse m kann man bei Anwendung der Definition der Dichte schreiben: m = ρ ⋅ V (2) Setzt man die Gleichungen (1) und (2) in die Gleichung für die Schwingungsdauer T ein , so erhält man: T = 2 π   2   ρ ⋅ V ρ ⋅ g ⋅ π ⋅ d 2 oder vereinfacht T = 2 π d   2   V g ⋅ π

Die letzte Gleichung kann man auch in anderer Form schreiben:

Setzt man für das Volumen der Flüssigkeit V = A ⋅ l = π ⋅ d 2 4 ⋅ l , dann erhält man: T = 2 π d ⋅ 2 π ⋅ d 2 ⋅ l 4 g ⋅ π Die Vereinfachung dieser Gleichung ergibt: T = 2 π   l 2 g

Das bedeutet: Die Schwingungsdauer einer Flüssigkeitssäule in einem U-Rohr ist nur von der Länge der Flüssigkeitssäule abhängig. Sie ist unabhängig davon, um was für eine Flüssigkeit es sich handelt, welchen Durchmesser das U-Rohr hat und wie stark die Flüssigkeit ausgelenkt wird. Aus der Gleichung kann man auch ableiten: Die Schwingungsdauer einer Flüssigkeitssäule mit der Länge l ist genauso groß wie die eines Fadenpendels der halben Länge.
Eine Gleichung für die Frequenz ergibt sich aus f = 1/T.
Praktisch genutzt werden die Schwingungen solcher Wassersäulen in Schlingertanks. Das sind Anordnungen auf Schiffen, die der Hin- und Herbewegung entgegenwirken.

Eine in einem U-Rohr hin- und herschwingende Flüssigkeit führt eine harmonische Schwingung aus.

Eine in einem U-Rohr hin- und herschwingende Flüssigkeit führt eine harmonische Schwingung aus.

Schwingungen eines Körpers, der in einer Flüssigkeit schwimmt

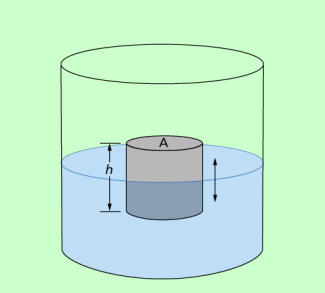
Ein zylinderförmiger Körper schwimmt in einer Flüssigkeit (Bild 2). Wird er ein Stück eingetaucht und dann sich selbst überlassen, so führt er Schwingungen in vertikaler Richtung aus.
Auch in diesem Falle kann man zunächst nachweisen, dass diese Schwingungen harmonisch sind. Eine harmonische Schwingung liegt dann vor, wenn die rücktreibende Kraft proportional zur Auslenkung ist. Die rücktreibende Kraft ist hier gleich der durch das Eintauchen zusätzlich auftretenden Auftriebskraft.
Für die Auftriebskraft gilt allgemein:

F A = ρ F l ⋅ V ⋅ g ρ F l Dichte der Flüssigkeit V verdrängtes Flüssigkeitsvolumen ( = Volumen des eingetauchten Teils des Körpers) g Ortsfaktor

Damit erhält man für die rücktreibende Kraft beim zusätzlichen Eintauchen des Körpers um die Strecke s:

F r ü c k = − ρ F l ⋅ Δ V K ⋅ g und mit Δ V K = A ⋅ s F r ü c k = −   ( ρ F l ⋅ A ⋅ g ) ⋅ s Es gilt also: F r ü c k ∼ s

Um eine Gleichung für die Schwingungsdauer herzuleiten, kann man wiederum von der allgemeinen Gleichung für die Schwingungsdauer einer harmonischen Schwingung ausgehen, die lautet:

T = 2 π   m D

Die Masse m des schwingenden Körpers ist:

m = ρ K ⋅ V K = ρ K ⋅ A ⋅ h (1)

Die Richtgröße D ergibt sich aus den Betrachtungen zur rücktreibenden Kraft zu:

D = ρ F l ⋅ A ⋅ g (2)

Damit erhält man für die Schwingungsdauer eines schwimmenden Körpers durch Einsetzen von (1) und (2):

T = 2 π ρ K ⋅ A ⋅ h ρ F l ⋅ A ⋅ g und nach Vereinfachung: T = 2 π ρ K ⋅ h ρ F l ⋅ g

Das bedeutet: Die Schwingungsdauer hängt von den Dichten von Flüssigkeit und Körper sowie von der Höhe des Körpers ab. Sie ist unabhängig von der Fläche des Körpers und von der Eintauchtiefe. Eine Gleichung für die Frequenz ergibt sich aus f = 1/T.

Ein in einer Flüssigkeit schwingender Körper gleichmäßiger Form führt eine harmonische Schwingung aus.

Ein in einer Flüssigkeit schwingender Körper gleichmäßiger Form führt eine harmonische Schwingung aus.

Schlingertank schwingende schwimmende Körper schwingende Flüssigkeitssäule Frequenz Auftriebskraft Schwingungen einer Flüssigkeitssäule Schwingungsdauer rücktreibende Kraft Schwingungen eines schwimmenden Körpers
Lexikon Share
Lernprobleme in Physik?
 

Mit deinem persönlichen Nachhilfe-Tutor Kim & Duden Learnattack checkst du alles. Jetzt 30 Tage risikofrei testen.

  • KI-Tutor Kim hilft bei allen schulischen Problemen
  • Individuelle, kindgerechte Förderung in Dialogform
  • Lernplattform für 9 Fächer ab der 4. Klasse
  • Über 40.000 Erklärvideos, Übungen & Klassenarbeiten
  • Rund um die Uhr für dich da
Jetzt in Physik durchstarten
Verwandte Artikel
alle anzeigen
Angaben zum Lexikon
Impressum
© Duden Learnattack GmbH, 2025

Einloggen