Zeigerdarstellung von Schwingungen
Schwingungen können in unterschiedlicher Weise dargestellt werden. Eine Möglichkeit besteht in der mathematischen Beschreibung mithilfe der Schwingungsgleichung .
Eine zweite Möglichkeit ist die Darstellung in y-t-Diagrammen, die man auch experimentell durch eine der vielfältigen Formen der Schwingungsaufzeichnung gewinnen kann.
Für harmonische Schwingungen gibt es noch eine dritte, recht anschauliche und leicht zu realisierende Möglichkeit, die Zeigerdarstellung. Dabei wird genutzt, dass man eine harmonische Schwingung als Projektion eines gleichförmig rotierenden Zeigers auf eine Achse auffassen kann.
Zeigerdarstellung von Schwingungen
Grundsätzliche Möglichkeiten der Darstellung von Schwingungen
Schwingungen können in unterschiedlicher Weise dargestellt werden. Eine Möglichkeit besteht in der mathematischen Beschreibung mithilfe der Schwingungsgleichung .
Eine zweite Möglichkeit ist die Darstellung in y-t-Diagramme
n, die man auch experimentell durch eine der vielfältigen Formen der Schwingungsaufzeichnung gewinnen kann.
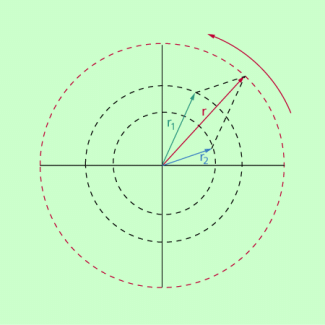
Für harmonische Schwingungen gibt es noch eine dritte, recht anschauliche und leicht zu realisierende Möglichkeit, die Zeigerdarstellung. Dabei wird genutzt, dass man eine harmonische Schwingung als Projektion eines gleichförmig rotierenden Zeigers auf eine Achse auffassen kann (Bild 1).
-
Eine harmonische Schwingung kann man als Projektion eines gleichförmig rotierenden Zeigers auf die y-Achse auffassen.
Die Zeigerdarstellung
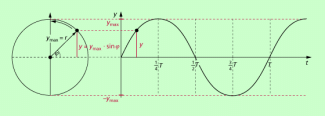
Wir betrachten zunächst den allgemeinen Fall einer Zeigerdarstellung (Bild 2). Zum Vergleich ist das entsprechende y-t-Diagramm mit angegeben. Dann gilt:
| – | Der Zeiger rotiert stets gleichförmig in mathematisch positivem Sinn, also entgegen der Uhrzeigerrichtung. Die Zeigerspitze durchläuft folglich die in Bild 1 hervorgehobenen Positionen 1, 2, 3, 4 und 5 nacheinander. |
| – | Die Länge des Zeigers r ist gleich der Amplitude: |
| – | Die Projektion des Zeigers auf eine vertikale Achse ist gleich der jeweiligen Elongation (Auslenkung). So hat z.B. der in Bild 2 dargestellte Zeiger zum gezeichneten Zeitpunkt t = 0 die Elongation y. In Stellung 2 wäre die Elongation maximal, in Stellung 3 null. |
| – | Eine vollständige Schwingung entspricht einer vollständigen Drehung des Zeigers. Zwischen dem Drehwinkel und der Umlaufzeit besteht damit folgender Zusammenhang: |
| – | Der Phasenwinkel zum Zeitpunkt t = 0 ist der Winkel . |
| – | Die Geschwindigkeit, mit der der Zeiger rotiert, muss gesondert angegeben werden. |
-
Zeigerdarstellung einer harmonischen Schwingungen für den allgemeinen Fall. Der Zeiger ist für den Zeitpunkt t = 0 gezeichnet.
Eine vereinfachte Zeigerdarstellung
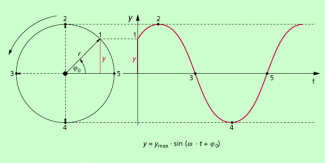
In den Bildern 1 und 2 ist die Zeigerdarstellung immer in Kombination mit einem y-t-Diagramm angegeben. Kennt man das Prinzip der Zeigerdarstellung, dann kann man eine wesentlich einfachere Möglichkeit wählen: Es wird lediglich der Zeiger in seiner Länge und Lage dargestellt, so wie das in Bild 3 gezeichnet ist. Diese Darstellung ist gewöhnungsbedürftig, aber sehr effektiv. Zum Vergleich ist deshalb das entsprechende y-t-Diagramm mit angegeben. Darauf könnte man aber verzichten. die Zeiger kann man nebeneinander oder untereinander zeichnen.
-
y-t-Diagramm und verkürzte Zeigerdarstellung
Überlagerung von Schwingungen in der Zeigerdarstellung
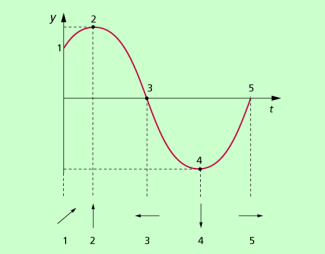
Überlagern sich zwei harmonische Schwingungen gleicher Frequenz, so ergibt sich wieder eine harmonische Schwingung. Das Zeigerdiagramm ermöglicht in einfacher Weise die Kennzeichnung der resultierenden harmonischen Schwingung (Bild 4):
| |
|
Aus dieser Betrachtung ergeben sich auch sofort zwei Spezialfälle:
| |
|
|
Sind die Frequenzen von zwei Schwingungen unterschiedlich, so rotieren die Zeiger mit unterschiedlicher Geschwindigkeit. Damit ändert sich auch ihre Lage zueinander ständig. Genauere Informationen zu diesem Fall einer Schwebung sind unter dem Stichwort „Überlagerung von Schwingungen“ gegeben.
-
Ermittlung der Länge des resultierenden Zeigers: Er ergibt sich durch vektorielle Addition der Einzelzeiger.