Federschwinger
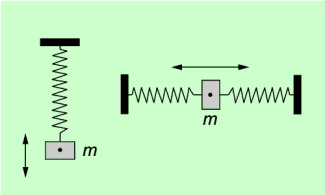
Man unterscheidet zwischen vertikalen und horizontalen Federschwingern (Bild 1).
Beispiele für schwingende Körper, die man vereinfacht als Federschwinger betrachten kann, sind Federungen von Autos und Motorrädern, ein Kranseil mit einer angehängten Last, eine Stimmgabel oder ein Trampolin mit Springer.
Schwingungsdauer und Frequenz eines Federschwingers
Die Schwingungsdauer (Periodendauer) eines Federschwingers hängt von der Masse des Pendelkörpers und von den elastischen Eigenschaften der Feder ab. Für die Schwingungsdauer eines Federschwingers gilt:
Beachte:
Die Ausdehnung der Feder hat keinen Einfluss auf die Schwingungsdauer, wenn man sich im elastischen Bereich der Feder befindet, also in dem Bereich, in dem das hookesche Gesetz gilt.
Da zwischen der Schwingungsdauer und der Frequenz der Zusammenhang
besteht, erhält man für die Frequenz eines Federschwingers die Gleichung:
Vertikaler und horizontaler Federschwinger
Material zum Thema
Kennzeichnung der Schwingung eines Federschwingers
Im elastischen Bereich der Feder führt ein Federschwinger harmonische Schwingungen oder sinusförmige Schwingungen aus. Wird der Pendelkörper nur einmal ausgelenkt, so verringert sich allmählich infolge des Luftwiderstandes und anderer Reibungseffekte die Amplitude. Die Schwingung ist dann gedämpft.
Bei einem Federschwinger wird ständig potenzielle in kinetische Energie umgewandelt und umgekehrt. Durch Reibung verringert sich die mechanische Energie allmählich.
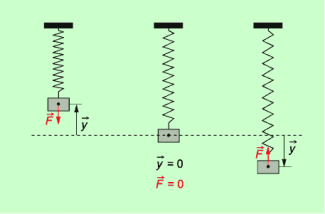
Rücktreibende Kräfte sind jeweils die elastischen Kräfte der Feder bzw. die Gewichtskraft (Bild 2).
Der Schwinger kann auch an mehreren Federn befestigt sein, wobei man diese Federn parallel oder hintereinander befestigen kann. Man spricht dann analog zur Schaltung von Widerständen in der Elektrizitätslehre von einer Reihenschaltung oder einer Parallelschaltung.
Für die Reihenschaltung von Federn gilt:
Für die Parallelschaltung von Federn gilt:
Auslenkung und rücktreibende Kraft bei einem vertikalen Federschwinger
Federpendel Schwingungsdauer eines Federschwingers horizontaler Federschwinger Frequenz eines Federschwingers Berechnung vertikaler Federschwinger Federschwinger Simulation Reihenschaltung von Federn Rechenbeispiel Parallelschaltung von Federn hookesches Gesetz
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 