Selbstorganisation
In der Natur kann man die Ausbildung vielfältiger Strukturen (Kristalle, Zellen, Wirbel, Wolkenformen) beobachten. Dabei bilden sich unter bestimmten Bedingungen aus zunächst unstrukturierten oder wenig strukturierten Zuständen Strukturen heraus. Da diese Vorgänge von selbst ablaufen, wenn die erforderlichen Bedingungen vorliegen, spricht man von Selbstorganisation. Die Theorie der Selbstorganisation, die ab etwa 1970 entwickelt wurde, bezeichnet man auch als Synergetik. Gegenstand der Synergetik ist die Erforschung der spontanen Bildung von Strukturen. Selbstorganisation bedeutet eine Erhöhung der Ordnung im System, die mit einer Entropieminderung verbunden ist.
Selbstorganisation als Grundlage der Evolution
In der Natur kann man die Ausbildung vielfältiger Strukturen (Kristalle, Zellen, Wirbel, Wolkenformen) beobachten. Dabei bilden sich unter bestimmten Bedingungen aus zunächst unstrukturierten oder wenig strukturierten Zuständen in einer Folge von irreversiblen Vorgängen Strukturen in Teilsystemen oder in einem Gesamtsystem heraus. Da diese Vorgänge von selbst ablaufen, wenn die erforderlichen Bedingungen vorliegen, spricht man von Selbstorganisation. Die Theorie der Selbstorganisation wird auch als Synergetik bezeichnet. Diese Theorie wurde ab etwa 1970 entwickelt. Wesentlichen Anteil daran hatten die Brüsseler Schule um den in Russland geborenen Physikochemiker ILYA PRIGOGINE (1917-2003, Nobelpreis 1977), die sowjetische Schule in Moskau und die Stuttgarter Schule um den Physiker HERMANN HAKEN (*1927).
Gegenstand der Theorie der Selbstorganisation ist die Erforschung der spontanen Bildung von Strukturen. Diese spontane Strukturbildung ist eine entscheidende Grundlage der Evolution.
Bedingungen für das Entstehen von Strukturen
Aus thermodynamischer Sicht geht Strukturbildung in offenen Systemen vor sich, also in Systemen, bei denen über die Systemgrenze hinweg ein Transport von Stoff und Energie erfolgen kann. Mit Energie und Stoffen wird auch Entropie transportiert. Beispiele für solche offenen Systeme sind tierische oder pflanzliche Zellen, Pflanzen, der Planet Erde oder ein Mensch.
Analysiert man die Bedingungen für das Entstehen von Strukturen genauer, so zeigt sich, dass Strukturbildung vorrangig in zwei Bereichen vor sich geht:
| – | Strukturen, die sich bei Wärmeabgabe oder tiefen Temperaturen bilden, |
| – | Strukturen, die fernab vom thermodynamischen Gleichgewicht entstehen. |
Wir betrachten nachfolgend Beispiele für die jeweiligen Bereiche und formulieren anschließend jeweils die allgemeinen Bedingungen und Merkmale.
Strukturbildung unter Wärmeabgabe
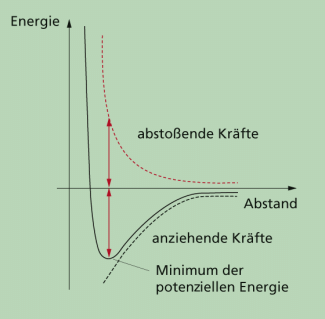
In einem Glas werden bei einer Temperatur von ca. 80 °C in 100 g Wasser etwa 50 g Kochsalz gelöst. Wird diese Lösung anschließend auf Zimmertemperatur abgekühlt, so bilden sich an einem Faden, der in der Flüssigkeit hängt, Salzkristalle. Durch die Wärmeabgabe verringert sich die kinetische Energie der Natrium- und Chlorid-Ionen. Wird ein einzelnes Chlorid-Ion betrachtet, so überlagern sich die abstoßenden Kräfte zwischen diesem und den anderen ebenfalls negativ geladenen Chlorid-Ionen mit den anziehenden Kräften zwischen dem Chlorid-Ion und den umgebenden positiv geladenen Natrium-Ionen.
Dadurch entsteht eine Energiepotenzialkurve um dieses Chlorid-Ion wie auch um jedes andere Ion in der Lösung. Wird die Lösung immer weiter abgekühlt, so nehmen die benachbarten Ionen den Ort minimaler potenzieller Energie an (Bild 4). Anziehende und abstoßende Kräfte sind dann gleich groß. Da diese Energiepotenzialkurve symmetrisch um das betrachtete Chlorid-Ion verläuft, kommt es zur Ausbildung regelmäßiger Abstände zwischen einer großen Anzahl von Ionen. Dadurch wird die Struktur makroskopisch als Kristall sichtbar. Da sich die Ordnung des Systems während der Kristallbildung erhöht, bedeutet das eine Verkleinerung der Entropie, also der Unordnung. Während der Kristallbildung wird Entropie exportiert.
Als Bedingungen für eine weitverbreitete Form von Strukturbildung kann man formulieren:
| – | Das betrachtete System gibt Energie in Form von Wärme an die Umgebung ab. |
| – | Das betrachtete System exportiert Entropie. |
Hat sich das strukturierte System, in unserem Fall ein Kochsalzkristall, einmal herausgebildet, dann besitzt es die folgenden charakteristischen Merkmale:
| – | Das System befindet sich im statischen und thermodynamischen Gleichgewicht. Es erfolgt auch kein Wärmeaustausch mit der Umgebung mehr. Solche Systeme bezeichnet man auch als konservative Systeme . |
| – | Durch die Gleichgewichtssituation kommen alle Vorgänge zum Erliegen. Insbesondere ändert sich die Entropie nicht mehr: |
| – | Die Struktur des Systems (Kristallform) ist nur durch ihre Bauelemente (Art der Ionen) vorgegeben und wird sich stets wieder genauso einstellen. |
| – | Der Vorgang der Kristallbildung ist reversibel, d. h. er kann rückgängig gemacht werden. |
Diese Art der Strukturbildung im thermodynamischen Gleichgewicht findet man in der Natur recht häufig, z. B. beim Kondensieren, beim Erstarren oder bei der Bildung von Mineralien, Schneeflocken und Eiskristallen.
-
Energiepotenzialkurve und Kräfte zwischen Ionen: Bei größerem Abstand überwiegen die anziehenden Kräfte, bei kleinerem Abstand die abstoßenden Kräfte.
Strukturbildung fernab vom Gleichgewicht
Wir betrachten auch hier zunächst Beispiele und leiten daraus allgemeine Merkmale ab.
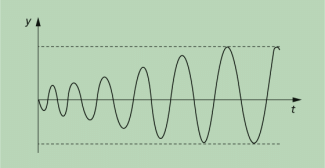
Schwingung einer Saite : Mit einem Bogen wird die Saite einer Geige gestrichen und damit zum Schwingen angeregt. Durch Reibungseffekte wird dabei dem System Saite Energie zugeführt. Die Saite wird beschleunigt und zugleich verdrillt. An einem bestimmten Punkt sind die rücktreibenden Kräfte so groß, dass sie die Haftreibungskraft überwinden. Die Saite schnellt zurück. Die rücktreibenden Kräfte werden an einer Stelle kleiner als die Reibungskraft, der Bogen greift wieder. Obwohl durch das Streichen der Saite dem System gleichförmig Energie zugeführt wird, stellt sich ein für das System charakteristischer Schwingungszustand ein, der sich aus einem Anfangszustand aufschaukelt und dann stabil bleibt (Bild 5). Der Saite wird Energie zugeführt, die sie als Schallenergie an die Umgebung abgibt.
-
Beim Streichen einer Saite nimmt die Amplitude der Schwingungen zu und erreicht dann einen stabilen Wert.
Strömungen in erwärmten Flüssigkeiten oder Gasen: Eine flache Flüssigkeitsschicht, die sich in einem Gefäß befindet, wird von unten erwärmt. Damit bildet sich eine Temperaturdifferenz zwischen dem unteren und dem oberen Rand heraus (Bild 6). Bei geringer Temperaturdifferenz wird Energie durch Wärmeleitung von unten nach oben transportiert. Verstärkt man die Energiezufuhr, so wächst die Temperaturdifferenz, und das System entfernt sich zunehmend vom thermodynamischen Gleichgewicht.
Die Schwerkraft wirkt an den oberen, kälteren und damit dichteren Schichten stärker als an den unteren. In der ganzen Flüssigkeit erscheinen Strudel und Wirbel. Wird eine bestimmte kritische Temperaturdifferenz erreicht, dann verlässt das System den chaotischen Zustand. Die Auftriebskräfte werden größer als die Reibungskräfte, es kommt zur Wärmeströmung. Eine winzige Bewegung eines Volumenelements nach oben oder nach unten entscheidet darüber, ob sich auch die darüber oder darunter liegenden Schichten in gleicher Weise bewegen. Schließlich bilden sich Konvektionszellen aus (Bild 6). Die mikroskopischen Fluktuationen (Schwankungen) haben sich durch Kopplung soweit verstärkt, das sie immer größere Raumbereiche erfüllen und schließlich makroskopisch sichtbar werden. Diese Erscheinung wird nach ihren Entdecker BÉNARD-Effekt genannt.
Die beschriebenen Konvektionszellen bilden je nach den gegebenen Bedingungen (Form des Gefäßes, Viskosität der verwendeten Flüssigkeit) unterschiedliche, das System charakterisierende Muster, die in einem bestimmten Temperaturbereich stabil bleiben.
Solche Konvektionszellen bilden sich in der Natur an verschiedenen Stellen heraus, z. B.
| in Form von Wolkenstraßen, | |
| als Konvektionsströmungen im Ozean, | |
| als großräumige Strömungen in der Konvektionszone der Erde. |
Die beschriebenen Zusammenhänge lassen sich auch relativ elementar mathematisch beschreiben, so wie das nachfolgend dargestellt ist.
Wird eine Flüssigkeitsschicht der Höhe d gleichmäßig von unten erwärmt, so bildet sich in diesem offenen System am Boden eine höhere Temperatur als in der übrigen Flüssigkeit heraus. Der Ausgleich dieses noch geringen Temperaturunterschiedes kann über Wärmeleitung erfolgen. Für die Wärme, die pro Zeiteinheit durch Leitung transportiert werden kann, gilt:
Dabei sind A die Grundfläche, d die Flüssigkeitshöhe, mit der Temperaturunterschied und die spezifische Wärmeleitfähigkeit der Flüssigkeit. Da die Wärmeleitfähigkeit von Flüssigkeiten und Gasen sehr gering gegenüber Festkörpern ist, verbleibt ein Teil der Wärme im unteren Teil der Flüssigkeit, leistet an ihr Volumenarbeit und führt zu einer Vergrößerung der Dichte gegenüber den darüber liegenden Flüssigkeitsschichten:
Das ist eine instabile Situation, die zum Ausgleich drängt:
| – | Ausgleich des Temperaturunterschiedes (System außerhalb des thermodynamischen Gleichgewichtes), |
| – | Ausgleich der auf die einzelnen Schichten wirkenden Kräfte (System außerhalb des statischen Gleichgewichts). |
Die Ausgleichsströmung wird jedoch durch die Viskosität (Zähigkeit) der Flüssigkeit behindert wird. Die Viskosität ruft eine Kraft hervor, die die Geschwindigkeitsunterschiede zwischen dem nach oben strömenden warmen und dem nach unten strömenden kalten Flüssigkeitsgebiet auszugleichen versucht. Dabei gilt:
Die Viskosität wirkt damit einer unmittelbaren Aufhebung der instabilen Situation entgegen. Setzt man die Energie, die den Konvektionsprozess antreibt, mit den Energieverlusten, die diesen Prozess hemmen, ins Verhältnis, so ergibt sich eine dimensionslose Zahl Ra (benannt nach RAYLEIGH, der als Erster Beziehungen für Instabilitäten in Flüssigkeiten untersucht hat):
Diese RAYLEIGH-Zahl Ra wird damit bestimmt durch
Materialkonstanten
| den Ausdehnungskoeffizienten | |
| die Wärmeleitfähigkeit | |
| die Viskosität | |
| die Dichte |
geometrische Verhältnisse
| die Höhe der Flüssigkeit d |
äußere Einflüsse
| die Erdbeschleunigung g | |
| die Temperaturdifferenz |
Gilt für die RAYLEIGH-Zahl Ra < 1, so tritt nur Wärmeleitung auf. Bei Ra > 1 setzt die Konvektion ein und die Wärmeströmung löst die Wärmeleitung ab. Untersuchungen haben gezeigt, dass für eine große Anzahl von Flüssigkeiten und Gasen der Übergang zur Konvektion bei derselben RAYLEIGH-Zahl einsetzt
Bei einer bestimmten kritischen Temperatur werden die Auftriebskräfte größer als die Reibungskräfte. Eine winzige Bewegung eines Volumenelements nach oben oder nach unten entscheidet darüber, ob sich auch die darüber und darunter liegenden Schichten in gleicher Weise bewegen. Die mikroskopischen Fluktationen (Schwankungen) haben sich durch Kopplung soweit verstärkt, dass sie immer größere Raumbereiche erfüllen und schließlich makroskopisch sichtbar werden. Es bilden sich Konvektionszellen aus. Für diese Ausgleichsströmungen sind alle möglichen Formen denkbar. Genauere Untersuchungen zeigen aber: Für eine bestimmte Flüssigkeit und eine gegebene Form des Gefäßes bildet sich jeweils ein typisches Konvektionsmuster heraus, das sich bei Wiederholung des Experiments unter gleichen Bedingungen immer wieder so einstellt.
Für solche am Beispiel beschriebene sich selbst organisierende Systeme lassen sich die folgenden allgemeinen Merkmale formulieren:
| Es liegen offene Systeme vor, also Systeme, bei denen über die Systemgrenze hinweg Energie und Entropie importiert bzw. exportiert werden. | |
| Dem System wird hochwertige Energie zugeführt und von diesem zur Selbstorganisation genutzt. Das System gibt entwertete Energie an die Umgebung ab. Daher werden solche Systeme auch als dissipative Systeme (Energie zerstreuende Systeme) bezeichnet. Der Energieimport und -export und der damit unter Umständen verbundene Stoffimport und -export ist ausgeglichen. Es gilt: | |
| Mit dem Import hochwertiger Energie erfolgt auch ein Entropieimport. Mit der Abgabe entwerteter Energie erfolgt ein Entropieexport. Darüber hinaus sind die Vorgänge im System nach dem 2. Hauptsatz der Thermodynamik mit Entropieproduktion verbunden. Damit ergibt sich als Bilanz für die Entropie des Systems: |
Da Selbstorganisation eine Erhöhung der Ordnung im System bedeutet und eine solche Veränderung stets mit einer Entropieminderung verbunden ist, gilt für den Prozess der Strukturbildung: Bei Strukturbildungen muss die Entropieänderung des Systems kleiner null sein; es muss also gelten:
Ist der Prozess der Strukturbildung abgeschlossen, so ändert sich die Entropie des Systems nicht mehr. Selbstorganisation ist demzufolge nur dann möglich, wenn ein System Entropie exportieren kann. Da die Entropie nicht nur ein Maß für die Unordnung, sondern auch für den Wert von Energie ist, kann ein System dann Entropie exportieren, wenn ihm hochwertige Energie zugeführt und minderwertige Energie von ihm abgegeben wird. Der Fall würde einen irreversiblen Prozess kennzeichnen.
Weiterhin sind für offene Systeme, in denen Selbstorganisation erfolgt, die nachfolgenden Merkmale kennzeichnend:
| Energietransformation : Im System erfolgen zahlreiche Energieumwandlungen, die zwar insgesamt zu einer Entwertung von Energie führen, immer aber auch damit verbunden sind, dass ein Teil der Energie in eine spezielle hochwertige Form umgewandelt wird. Diesen Sachverhalt kennzeichnet man mit dem Terminus Energietransformation. | |
| Gleichgewichtsferne : Selbstorganisation ist nur möglich, wenn der Abstand des Systems vom Gleichgewicht gewisse kritische Werte übersteigt. Man meint damit Zustände fernab vom thermodynamischen Gleichgewicht. | |
| Rückkopplung und Selbstverstärkung : Selbstorganisation ist in der Regel durch verschiedene Rückkopplungseffekte charakterisiert. Damit können minimale Veränderungen in den Bedingungen das Verhalten des ganzen Systems verändern. | |
| Kooperation : Besteht ein selbstorganisiertes System aus einzelnen Komponenten, so müssen diese miteinander kooperieren, damit sich das System herausbilden kann und erhalten bleibt. | |
| Symmetriebrechung : Die sich im System herausbildenden Strukturen sind ein Ausschnitt aus prinzipiell möglichen Strukturen. | |
| Stabilität : Selbstorganisierte Systeme sind relativ stabil gegenüber kleinen Störungen durch die Umgebung. Größere Störungen sind eine Gefahr für das System. Wegen der Existenz kritischer Werte können sie zum Zusammenbruch der ganzen Struktur führen. |
Nachfolgend werden einige weitere Beispiele für sich selbst organisierende Systeme genannt und erläutert.
Der Motor der Evolution auf der Erde
Unsere Erde befindet sich in einem Strahlungsgleichgewicht. Das bedeutet: Sie gibt genauso viel Energie an den umgebenden Weltraum ab wie sie von der Sonne aufnimmt. Es handelt sich dabei in jeder Sekunde um etwa .
Die von der Erde aufgenommene Energie ist aufgrund der hohen Temperatur der Strahlungsquelle Sonne hochwertig. Mit ihrer Aufnahme ist ein Entropieimport verbunden. Es gilt:
Durch die vielfältigen Prozesse auf der Erde wird die hochwertige Energie, die von der Sonne kommt, entwertet. Die Abgabe von Energie an den umgebenden Weltraum erfolgt bei einer Temperatur von etwa 260 K. Das ist die Temperatur der Erdoberfläche, die ein Beobachter aus großer Höhe messen würde. Damit ergibt sich für den Entropieexport der Erde:
Der Vergleich der Entropiewerte zeigt: Der Export von Entropie übersteigt den Entropieimport etwa um das 20-fache. Die Erde gibt im Mittel in jeder Sekunde folgende Entropie ab:
Der Entropieexport und damit die Entwertung von Energie ist die Voraussetzung für die vielfältigen Prozesse der Selbstorganisation auf der Erdoberfläche und in der Atmosphäre, z. B. für
| den Wasserkreislauf, | |
| das Wettergeschehen, | |
| die Entwicklung von Leben. |
Aus dem Zusammenhang zwischen Selbstorganisation und Entropieexport (Entwertung von Energie) kann man auch schließen, dass es Leben im Weltall (außerirdisches Leben) nur in der Nähe hochwertiger Energiequellen (Sterne) geben kann. Fernab der Sonne oder anderer Sterne können sich keine lebenden Strukturen entwickeln, weil dort zu wenig hochwertige Strahlungsenergie zur Verfügung steht. Tatsächlich hat man auf sonnenfernen Planeten bislang noch keinerlei Lebensformen entdeckt.
Der Mensch als thermodynamisches System
Physikalisch betrachtet ist der Mensch ein komplexes, hoch organisiertes, offenes System. Betrachtet man nur den Grundumsatz des Menschen, also die zur Aufrechterhaltung der Lebensfunktionen notwendige Energie, so nimmt der Mensch im Durchschnitt 6 500 kJ pro Tag zu sich. Die von ihm aufgenommene Energie ist hochwertige Energie in den organischen Substanzen der Lebensmittel. Diese stammt letztendlich aus der Energie der Sonnenstrahlung, die über die Fotosynthese in den pflanzlichen Zellen und durch die Nahrungsketten in die tierischen Nahrungsmittel gelangt. Diese Energie wird durch den Verdauungsprozess entwertet. Damit ist eine Entropieerhöhung (Vergrößerung der Unordnung) verbunden.
Mit der Abgabe der entwerteten Energie an die Umgebung (Wärmestrahlung, Ausscheidungen) wird auch die erzeugte Entropie exportiert. Der Entropieexport eines Menschen kann mit folgender Gleichung berechnet werden:
Das ist der Entropieexport eines Menschen, bezogen auf den Grundumsatz. Dieser Entropieexport ist die Voraussetzung dafür, dass sich ein Mensch entwickeln kann.
Die BELOUSOV-ZHABOTINSKI-Reaktion
Bei „gewöhnlichen“ chemischen Reaktionen verbinden sich z. B. zwei Stoffe zu einem neuen, stabilen Stoff. Daneben gibt es eine Reihe von chemischen Reaktionen, die nicht zu einem stabilen Zustand führen, sondern die durch periodische Veränderungen gekennzeichnet sind. Man spricht von selbst erregten Oszillationen. Solche Oszillationen sind schon seit langem bekannt und wurden früher als Kuriositäten angesehen. In einer Arbeit von 1832, veröffentlicht in POGGENDORFs Annalen, heißt es:
„Eine kleine Flasche, welche etwas Phosphor enthielt, wurde eine Zeitlang als Feuerzeug gebraucht, ... ich bemerkte zufällig, dass sie dann und wann im Dunkeln ein ziemlich intensives Licht von sich gab. Dieses Phänomen machte mich aufmerksam und bald nahm ich wahr, dass sich das Leuchten ganz regelmäßig zu jeder siebenden Secunde wiederholte.“
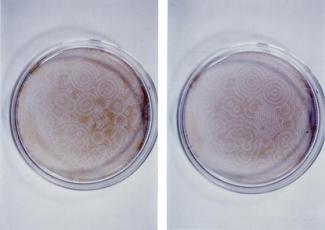
Die vielleicht berühmteste Reaktion dieser Art, die zugleich auch eine der farbenfreudigsten ist, wird nach ihren russischen Entdeckern BELOUSOV-ZHABOTINSKI-Reaktion genannt. Bei dieser Reaktion organisieren sich die zufälligen chaotischen Bewegungen der Moleküle spontan in räumlich-zeitlichen Strukturen. Die geringste Schwankung in einem Teil der Lösung kann dabei verstärkt werden. Kommt es an einer Stelle zu einer zufälligen Anhäufung „roter“ Moleküle, so fördern diese durch Autokatalyse die Erzeugung weiterer „roter“ Moleküle. So werden sich in einem gewissen Bereich die „roten“, in einem anderen die „blauen“ Moleküle verstärken. Dadurch entstehen großräumige und zeitlich veränderliche Strukturen verschiedener Chemikalien.
Diese Strukturen lassen sich mitunter auf recht einfache Weise erzeugen (Bild 11). Man kennt inzwischen viele Reaktionen, die einer Selbstorganisation unterliegen.
Es wird vermutet, dass Reaktionen dieser Art schon in der Frühzeit der Erde vorkamen. Dann wäre das Hervorbringen einer sich selbst reproduzierenden Sequenz von Aminosäuren als Träger genetischer Informationen nicht nur dem Zufall überlassen geblieben.
-
Die räumlich-zeitlichen Veränderungen beim Umschlagen der Reaktion breiten sich als sogenannte chemische Wellen durch die Lösung aus.
Oliver Schwarz
Suche nach passenden Schlagwörtern
- Sonnengranulation
- Stoff
- Strukturbildung
- Energieimport
- Energieexport
- selbst erregte Oszillationen
- Stabilität
- Entropie
- Gleichgewichtsferne
- konservative Systeme
- Mensch als thermodynamisches System
- dissipative Systeme
- Energie
- Energietransformation
- Entropieproduktion
- Entropieimport
- Kooperation
- Synergetik
- Benard-Effekt
- Hermann Haken
- thermodynamisches Gleichgewicht
- Fluktuationen
- spontane Bildung von Strukturen
- Symmetriebrechung
- Selbstverstärkung
- Ilya Prigogine
- offene Systeme
- Rückkopplung
- Entropieexport
- Schwankungen
- Gleichgewichtszustand
- BELOUSOV-ZHABOTINSKI-Reaktion
- Benardeffekt
- Grundumsatz des Menschen

