- Lexikon
- Physik Abitur
- 2 Mechanik
- 2.2 Kinematik
- 2.2.6 Überlagerung von Bewegungen
- Würfe im Sport
Würfe im Sport
So soll z. B. beim Speerwerfen eine möglichst große Weite erzielt werden. Das erfordert eine möglichst große Abwurfgeschwindigkeit und einen optimalen Abwurfwinkel, der wiederum u. a. von den herrschenden Windverhältnissen abhängig ist.
Beim Stabhochsprung ist entscheidend, den gesamten Körper mithilfe eines langen Stabes über eine maximale Höhe zu bringen (Bild 2). Demzufolge muss hier die nach oben gerichtete Geschwindigeitskomponente möglichst groß sein und zugleich durch geschickte Körperbewegungen erreicht werden, dass die Latte nicht heruntergerissen wird.
Kugelstoßen, Hochsprung und Weitsprung
Beim Kugelstoßen sowie beim Hochsprung und beim Weitsprung können die Gesetze des schrägen Wurfs angewendet werden, weil in diesen Fällen der Luftwiderstand vernachlässigt werden kann. Trotzdem sind auch bei diesen Sportarten Besonderheiten zu beachten.
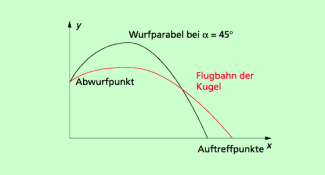
Beim Kugelstoßen liegt der Abwurfpunkt höher als der Auftreffpunkt (Bild 3). Das hat zu Folge, dass bei bestimmter Abwurfgeschwindigkeit und Abwurfhöhe die maximale Wurfweite nicht bei einem Abwurfwinkel von 45° erreicht wird, sondern bei einem Winkel von etwa 35°.
Beim Stabhochsprung ist aus physikalischer Sicht die Bewegung des Schwerpunktes (Massemittelpunktes) des menschlichen Körpers entscheidend. Damit liegt der „Abwurfpunkt“ nicht in Höhe des Erdbodens, von dem aus die Höhe gemessen wird, sondern etwa in der Körpermitte. Die Höhe, in die der Körperschwerpunkt gehoben wird, ist somit wesentlich geringer als die Höhe, die als Sprunghöhe angegeben wird.
Beim Weitsprung liegen zwar der Absprungpunkt und der Auftreffpunkt etwa in gleicher Höhe. Entscheidend ist aber auch hier die Bewegung des Körperschwerpunktes, der sich über der Absprungstelle befindet. Durch geschickte Körperbewegungen beim Landen (Vorstrecken der Beine) kann eine Vergrößerung der Sprungweite erreicht werden.
Die Weite beim Kugelstoßen hängt von der Abwurfhöhe, der Abwurfgeschwindigkeit und dem Abwurfwinkel ab.
Diskuswerfen und Skispringen
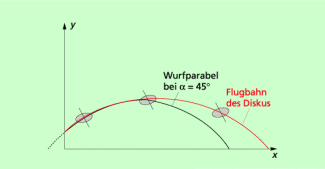
Beim Diskuswerfen erhält der Diskus beim Abwurf einen Drall. Seine Drehachse behält dadurch während des Fluges ihre räumliche Lage näherungsweise bei (Bild 4). Vor allem in zweiten Teil der Flugbahn wirkt aufgrund der Lage des Diskus ein „Luftpolster“. Dadurch wird erreicht, dass der Diskus langsamer zu Boden sinkt und weiter fliegen kann, als die Wurfparabel reicht. Besonders günstig ist leichter Gegenwind. Als optimal hat sich beim Diskuswerfen ein Abwurfwinkel von 33° bis 35° erwiesen.
Ein ähnlicher Effekt tritt beim Skispringen auf. Der Skispringer nimmt nach dem Absprung eine solche Haltung ein, dass die Ski und sein Körper eine möglichst große Fläche bilden und er damit auf einem Luftpolster „schwebt“. Besonders groß ist dieser Effekt, wenn Wind mit nicht zu großer Geschwindigkeit von vorn weht.
Beim Diskuswerfen spielt die Luft eine „tragende Rolle“.
Speerwerfen, Golfen, Fußball
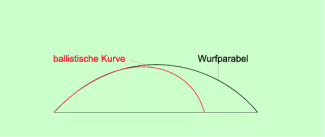
Beim Speerwerfen, beim Abschlagen eines Golfballs oder beim Abschlagen eines Fußballs hat der Luftwiderstand erheblichen Einfluss auf die Wurfbahn. Die Bahn ist eine ballistische Kurve, die erheblich von einer Wurfparabel abweicht (Bild 5). Die Wurfweite ist somit wesentlich kleiner als diejenige, die man bei einem idealen schrägen Wurf erhalten würde. Genauere Untersuchungen zeigen, dass man ohne Wind die größten Weiten nicht bei einem Abwurfwinkel von 45° erzielt, sondern bei Abwurfwinkeln, die zwischen 30° und 40° liegen. Experimentelle Untersuchungen bei Fußbällen ergaben z. B. bei einer Abschussgeschwindigkeit von 45 m/s folgende Wurfweiten:
bei 30°: 56,8 m
bei 35°: 57,6 m
bei 40°: 57,2 m
bei 45°: 55,7 m
Das sind bei 45° nur etwa 27 % der Wurfweite, die man erhält, wenn man die Gesetze des schrägen Wurfs anwendet. Das zeigt: Bei vielen Würfen im Sport sind die Gesetze des schrägen Wurfs nicht anwendbar, weil der Luftwiderstand entscheidenden Einfluss auf die Bahnkurve und damit auch auf die Wurfweite hat.
Experimentelle Untersuchungen und Erfahrungswerte bestimmen entscheidend die Bedingungen, die ein Sportler einzuhalten sollte, wenn er maximale Weiten erreichen will.
Wurfparabel und ballistische Kurve
Skispringen ist eine Sportart, bei der es darum geht, eine möglichst große Weite zu erzielen (Bild 1). Daher versucht der Springer in der Anlaufspur eine möglichst große Geschwindigkeit zu erreichen, kräftig vom Schanzentisch abzuspringen und durch eine geschickte Körperhaltung ein Luftpolster für einen möglichst weiten Flug zu nutzen.
Analyse eines Sprunges
Im Anlauf versucht der Springer eine möglichst hohe Geschwindigkeit zu erzielen. Die maximale Geschwindigkeit, die am Schanzentisch erreicht wird, hängt u. a. von der Anlauflänge, von den Bedingungen in der Anlaufspur, vom Material und von der Körperhaltung des Springers ab. Die erreichten Geschwindigkeiten liegen bei der unten beschriebenen Schanze um 90 km/h.
Am Schanzentisch versucht der Springer möglichst kräftig abzuspringen. Das sollte möglichst nah am Ende des Schanzentisches erfolgen.
Da der Schanzentisch nach unten geneigt ist und der Springer schräg nach vorn abspringt, kann die Bewegung zumindest in ihrer Anfangsphase näherungsweise als waagerechter Wurf angesehen werden.
Nach dem Absprung versucht der Springer möglichst schnell eine solche Haltung einzunehmen, dass er zusammen mit seinen Ski eine möglichst große Fläche bildet und so auf einem Luftpolster „schwebt“. Die Schanze ist so konstruiert, das sich der Springer während seines Fluges nicht vom Aufsprunghügel entfernt, sondern ihm allmählich näherkommt. Das ist auch eine Frage der Sicherheit.
Die „normalen“ Weiten liegen um den Normpunkt herum. Bei größeren Weiten wird eine sichere Landung aufgrund des Bahnverlaufs schwieriger, hinter dem kritischen Punkt K sehr problematisch. Die Sprungweite wird längs des Aufsprunghügels gemessen, wobei der Nullpunkt der Fußpunkt des Schanzentisches ist.
Die durchschnittliche Flugdauer eines Skispringers wird meist überschätzt. Sie beträgt in der Regel 2,5 s bis 3,5 s.
Ein Skispringer während seines Fluges
Würfe im Sport - Skispringer
Schäfer, Michael, Huettenberg-Weidenhausen
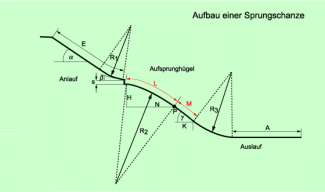
Aufbau einer Sprungschanze
Eine Sprungschanze besteht aus einem Anlauf mit dem Absprungtisch, einem Aufsprunghügel und einem Auslauf (Bild 2). Die folgenden Angaben beziehen sich auf die Sprungschanze in Oberstdorf.
Beim Anlauf beträgt die maximale Anlauflänge E = 82 m. Die Bahn des Anlaufturms hat einen Neigungswinkel von 37°. Der Schanzentisch ist 11,5° nach unten geneigt. Der Radius ist nicht konstant, sondern nimmt zu und beträgt 80 m bis 100 m. Die Höhe des Schanzentisches über dem Aufsprunghügel beträgt 2,5 m.
Der Aufsprunghügel ist bis zum Punkt P, dem Normpunkt, gekrümmt. Der Radius nimmt ebenfalls zu und hat einen Wert von 150 m bis 240 m. Die Aufsprungbahn vom Fußpunkt des Schanzentisches bis zum Normpunkt P ist L = 70 m lang. Anschließend folgt bis zum kritischen Punkt K ein gerades Bahnstück mit einer Länge von
M = 15 m. Es hat eine Neigung von 37°, also die gleiche Neigung wie die Bahn des Anlaufturms. Damit ist die gesamte Bahn vom Schanzentisch bis zum kritischen Punkt K ca. 85 m lang. Der Höhenunterschied H zwischen dem Fußpunkt des Schanzentisches und dem Normpunkt P beträgt H = 33,2 m, die entsprechende horizontale Entfernung
N = 62,5 m.
Der Auslauf ist gekrümmt und hat einen Radius = 115 m. Er geht in einen geraden Teil A über.
Normalschanzen, Großschanzen und Sprungweiten
Als Normalschanzen werden Sprungschanzen bezeichnet, bei denen die Sprungweiten bis etwa 90 m liegen. Schanzen, die größere Flugweiten ermöglichen, werden als Großschanzen bezeichnet. Einige Anlagen ermöglichen besonders weite Flüge bis zu 200 m. Solche Anlagen nennt man Skiflugschanzen. Die größten Anlagen dieser Art befinden sich in Planica (Slowenien), Bischofshofen (Österreich) und Vikersund (Schweden). Einige wichtige Meilensteine im Skisprung waren:
- 1936 erreichte der Österreicher Sepp Bradl in Planica erstmals mit 101,5 m eine Sprungweite von über 100 m.
- 1954 stattete der DDR-Trainer Hans Renner eine Schanze in Zella-Mehlis (Thüringen) mit Platten aus, die auch ein Training im Sommer ermöglichten.
- 1987 zeigte der Schwede Jan Bokloev erstmals den V-Stil, den heute alle Springer anwenden.
- 1994 flog der Finne Toni Nieminen als Erster mit 203 m auf über 200 m. Kurz zuvor hatte das auch der Österreicher Andreas Goldberger mit 202 m geschafft, griff aber in den Schnee, sodass dieser Flug als gestürzt galt.
- 1997 erreichte der Norweger Lasse Ottesen mit 212 m in Planica einen neuen Weltrekord, der gegenwärtig auch noch gilt.
Aufbau einer Sprungschanze
Ein Angebot von 