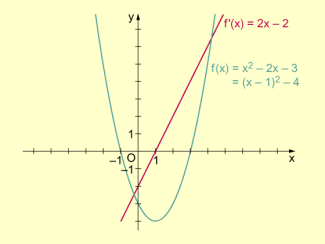Der Satz von ROLLE

Der nach dem französischen Mathematiker MICHEL ROLLE (1652 bis 1719) benannte Satz besagt Folgendes:

• Ist eine Funktion f im abgeschlossenen Intervall $\left[a;b\right]$ stetig und im offenen Intervall $\left]a;b\right[$ differenzierbar mit $f\left(a\right)=f\left(b\right)$, dann existiert mindestens eine Stelle c zwischen a und b, also $c\in \left]a;b\right[$, so dass $f^{\prime }\left(c\right)=0$ ist.

Beweis des Satzes von ROLLE

Man unterscheidet beim Beweis zwei Fälle.

1. Fall: f ist in $\left[a;b\right]$ konstant
   Es gilt also $f\left(x\right)=k$ für jedes $x\in \left[a;b\right]$ und damit $f^{\prime }\left(x\right)=0$ für alle $x\in \left[a;b\right]$.
2. Fall: f ist in $\left[a;b\right]$ nicht konstant

Ohne Beschränkung der Allgemeinheit gelte für die Funktionswerte $f\left(x\right)>f\left(a\right)füra<x<b$. Da f in $\left[a;b\right]$ stetig ist, nimmt f in $\left[a;b\right]$ einen größten Wert $f\left(x_0\right)=M$ an.

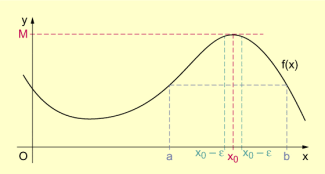
Für genügend kleines $h>0$ gilt:
$\begin{array}{l}f(x_0-h)-f(x_0)\le 0f(x_0+h)-f(x_0)\le 0\\ \frac{f(x_0+h)-f(x_0)}{-h}\ge 0\frac{f(x_0+h)-f(x_0)}{h}\le 0\end{array}$

Strebt h nun gegen null, so folgt hieraus $f^{\prime }\left(x\right)=0$.
Im Falle $f\left(x\right)<f\left(a\right)füra<x<b$ wird analog gefolgert.

Einen Spezialfall des Satzes von ROLLE erhält man für $f\left(a\right)=f\left(b\right)=0$:

• Zwischen zwei Nullstellen a und b einer Funktion f, die in $\left[a;b\right]$ stetig und in $\left]a;b\right[$ differenzierbar ist, liegt mindestens eine Nullstelle von $f^{\prime }\left(x\right)$.

Geometrisch bedeutet der Satz von ROLLE, dass es mindestens einen Kurvenpunkt in $\left]a;b\right[$ gibt, dessen Tangente parallel zur
x-Achse ist.

Wir betrachten noch zwei Beispiele zum Satz von ROLLE und zu seiner Anwendung.

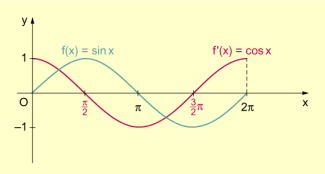
• Beispiel 1: Die Funktion $f\left(x\right)=\sin x$ ist ein Beleg dafür, dass man im Satz von ROLLE nicht formulieren darf, dass genau eine Zahl $x_{0}mita<x_0<bund{f}^{\prime }\left(x_0\right)=0$ existiere.

Betrachtet man $f\left(x\right)=\sin x$ in $\left[0;2\pi \right]$, dann erfüllt f die Voraussetzungen des Satzes von ROLLE. Die Ableitungsfunktion ist $f^{\prime }\left(x\right)=\cos x$. Für $f^{\prime }\left(x\right)=0$ erhält man $\cos x=0$, woraus $x_1=\frac{\pi }{2}und{x}_2=\frac{3\pi }{2}$ folgt.

• Beispiel 2: Für die Funktion $f(x)=x^2-2x-3$ ist im Intervall $\left[-2;4\right]$ eine Stelle $x_0$ so zu bestimmen, dass die Tangente in $x_0$ an die Funktion f parallel zur x-Achse ist.

Für $f^{\prime }\left(x\right)$ erhält man $f^{\prime }\left(x\right)=2x-2$. Aus $f^{\prime }\left(x\right)=0$ folgt $2x_0-2=0$ und demzufolge $x_0=1$.

Mit anderen Worten: An der Stelle $x_0=1$ besitzt die Funktion $f(x)=x^2-2x-3$ eine zur x-Achse parallele Tangente.