Dichtefunktion stetiger Zufallsgrößen

Beispiel: Lars experimentiert mit seiner Kugelbahn. Die über mehrere Kurven und verschiedene Hindernisse abwärts geführte Kugel rollt auf einer waagerechten Schiene aus. Lars stellt fest, dass sie bei den mehrfach durchgeführten Versuchen an verschiedenen Stellen zum Liegen kommt. Die Entfernung vom Beginn der waagerechten Rollschiene bis zu dem Punkt, an dem die Kugel anhält, ist eine Zufallsgröße X. Die Kugel rollt jedes Mal mindestens 150 cm, aber höchstens 250 cm weit, d.h., die Zufallsgröße X kann alle Werte aus dem Intervall [150; 250] annehmen.

Eine Zufallsgröße, die prinzipiell jeden Wert aus einer überabzählbaren Menge annehmen kann (sei es aus einem beschränkten Intervall oder aus der Menge $ℝ$), nennt man im Allgemeinen eine stetige Zufallsgröße. Dabei muss man beachten, dass der Begriff „stetige Zufallsgröße“ von dem Begriff der „stetigen Funktion“ (wie er in der Analysis verwandt wird) abweicht. Mit der Bezeichnung einer Zufallsgröße als stetig ist man lediglich darauf aus, dass die Wertemenge von X nicht diskret ist, sondern ein Kontinuum bildet. Mitunter wird deshalb auch von einer zufälligen reellen Zahl gesprochen.

Kehren wir nun zu obigem Beispiel zurück.
Beim Bestimmen der Wahrscheinlichkeitsverteilung von X stößt Lars auf eine Schwierigkeit. Die Werte von X bilden eine überabzählbar unendliche Menge und deshalb gilt $P\left(X=x\right)=0$, denn $P\left(X=x\right)$ kann keine von null verschiedene Zahl sein, da sonst die Summe aller Wahrscheinlichkeiten nicht gleich 1 wäre.

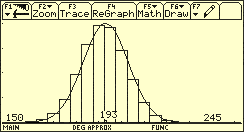
Die Wahrscheinlichkeitsverteilung von X lässt sich also nicht (wie bei einer diskreten Zufallsgröße) durch die Angabe der Einzelwahrscheinlichkeiten charakterisieren.

Eine von null verschiedene Wahrscheinlichkeit kann nur ein Ereignis besitzen, bei dem X in ein Intervall fällt, wobei dieses Intervall durchaus sehr klein sein kann wie etwa [196,7; 196,8].

Lars möchte aber noch kleinere Intervalle der Art $\left[x;x+\Delta x\right]$ betrachten, um $\Delta x$ gegen null gehen zu lassen, wie er es aus der Infinitesimalrechnung kennt. Dabei ist ihm bewusst, dass es sich um eine theoretische Abstraktion handelt, denn auch mit der genauesten Messmethode kann ein bestimmtes Minimum grundsätzlich nicht unterschritten werden.

Aufgrund seiner Messergebnisse vermutet Lars, dass gilt:
$\frac{P\left(x\le X\le x+\Delta x\right)}{\Delta x}\to f\left(x\right)für\Delta x\to 0(mitf\left(x\right)\ge 0)$

Anmerkung: Das unmögliche Ereignis besitzt die Wahrscheinlichkeit null. Ein Ereignis mit der Wahrscheinlichkeit null ist nicht zwangsläufig unmöglich.

• Eine Funktion f heißt Dichtefunktion oder einfach Dichte einer stetigen Zufallsgröße genau dann, wenn $f\left(x\right)\ge 0$ für alle $x\in ℝ$ und
  ${\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f\left(x\right)dx}=1$ gilt.

Eine stetige Zufallsgröße X kann dann als gegeben angesehen werden, wenn deren Dichtefunktion bekannt ist. Die Wahrscheinlichkeit $P\left(X\le a\right)$ berechnet sich als das Flächenintegral
$P\left(X\le a\right)={\displaystyle \underset{-\infty }{\overset{a}{\int }}f\left(x\right)dx}$.

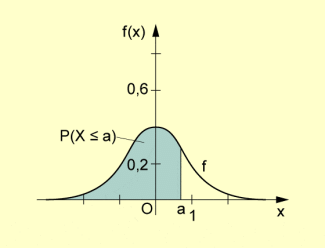
Der Begriff „Dichtefunktion“ ist dem physikalischen Sachverhalt einer stetigen Masseverteilung längs einer Geraden nachempfunden, bei dem es keine Massen gibt, die in bestimmten Punkten konzentriert sind, und wo man nur von Masse sprechen kann, die auf einem bestimmten Abschnitt der Geraden liegt.

Die Dichtefunktion f einer stetigen Zufallsgröße gibt die Wahrscheinlichkeitsmasse je Maßeinheit bzw. je Intervall an. Durch die Angabe einer Dichtefunktion ist es möglich, allen unüberschaubar vielen Intervallen von $ℝ$ jeweils eine Wahrscheinlichkeit zuzuordnen.

Ein großer Funktionswert $f\left(x\right)$ der zur Zufallsgröße X gehörenden Dichte f, d.h. eine hohe Dichte an der Stelle x, bringt aber auch zum Ausdruck, dass die empirischen Ergebnisse einer unabhängigen Versuchsserie zur Zufallsgröße X dort sehr dicht liegen werden.

Beachtet werden muss, dass $f\left(x\right)$ keine Wahrscheinlichkeit ist, im Unterschied zu $P\left(x\right)$ bei diskreten Verteilungen.

Beispiel 1: Gleichverteilung über dem Intervall [a; b] mit a < b

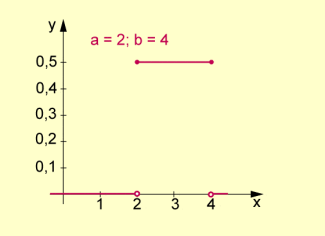
Die Funktion f mit
$f\left(x\right)=\{\begin{array}{cc}\frac{1}{b-a}& füra\le x\le b\\ 0& sonst\end{array}$
ist eine Dichtefunktion der Gleichverteilung über dem Intervall $\left[a;b\right]$, weil

1. aus $f\left(x\right)=\frac{1}{b-a}>0$ für $a\le x\le b$ (gilt wegen $b>a$) die Beziehung $f\left(x\right)\ge 0$ für alle $x\in ℝ$ folgt und
2. ${\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f\left(x\right)dx}=0+{\displaystyle \underset{a}{\overset{b}{\int }}\frac{1}{b-a}dx}+0=\frac{1}{b-a}\cdot \left(b-a\right)=1$ gilt.

Das Beispiel zeigt, dass die Dichtefunktion einer stetigen Zufallsgröße nicht notwendig eine stetige Funktion sein muss.

Beispiel 2: Exponentialverteilung mit dem Parameter $\lambda mit\lambda >0$

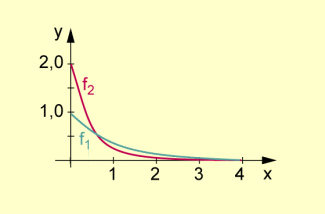
Die Funktion
$f_{\lambda }\left(x\right)=\{\begin{array}{cc}\lambda \cdot e^{-\lambda x}& fürx\ge 0\\ 0& fürx<0\end{array}$
ist eine Dichtefunktion der Exponentialverteilung, weil

1. $f_{\lambda }\left(x\right)\ge 0$ für alle $x\in ℝ$ (wegen $\lambda >0$) ist und
2. ${\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f\left(x\right)dx}=0+{\displaystyle \underset{0}{\overset{\infty }{\int }}\lambda e^{-\lambda x}dx}=-e^{-\lambda x}|\begin{array}{c}{}^{\infty }\\ {}_0\end{array}=1-\underset{x\to \infty }{\lim }{e}^{-\lambda x}=1-0=1$gilt.

Das Beispiel zeigt, dass es durchaus sinnvoll ist, Dichtefunktionen mit einem unbeschränkten Definitionsbereich zu betrachten, auch wenn es in der Praxis nicht möglich ist, beliebig große Werte der zugehörigen Zufallsgröße X zu messen.