Dreiecksverteilung (simpsonsche Verteilung)

THOMAS SIMPSON war von Beruf Weber. Seinen Lebensunterhalt verdiente er sich vor allem als Mathematiklehrer (zuerst an einer Abendschule in Derby und später an der Königlichen Militärakademie in London). Sein Hauptinteresse galt der Wahrscheinlichkeitsrechnung und der Analysis. Bekannt geworden ist er auch durch die simpsonsche Formel zur näherungsweisen Flächenberechnung.

Mit der Dreiecksverteilung diskreter Zufallsgrößen beschäftigte sich SIMPSON, um die in der damaligen Praxis übliche Verwendung des arithmetischen Mittels zum Messfehlerausgleich als gerechtfertigt nachzuweisen. Er zeigte, dass diese Verfahrensweise sinnvoll ist, wenn die Häufigkeiten von n äquidistanten diskreten Messwerten ein Dreieck bilden, wenn also z.B. gilt:

Vergleiche dazu auch die folgende Abbildung.

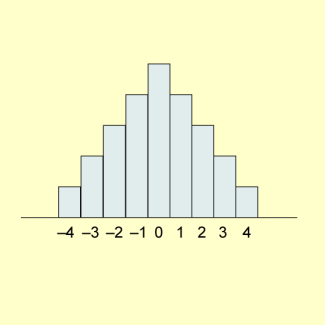
Diesen Ansatz für eine diskrete Dreiecksverteilung kann man auf stetige Wahrscheinlichkeitsverteilungen ausdehnen.

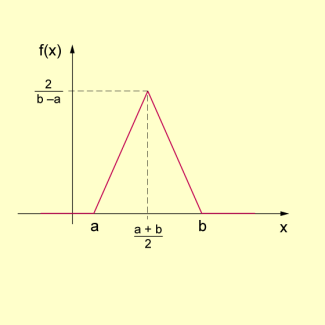
• Definition: Eine stetige Zufallsgröße X heißt dreiecksverteilt über dem Intervall $\left[a;b\right]$, wenn sie die Wahrscheinlichkeitsdichte f mit
  $f\left(x\right)=\{\begin{array}{cc}\frac{2}{b-a}\cdot \left(1-\frac{2}{b-a}\cdot \left|x-\frac{a+b}{2}\right|\right)& füra\le x\le b\\ 0& sonst\end{array}$
  besitzt, d.h. wenn der Graph von f die Form eines gleichschenkligen Dreiecks hat.

Für eine dreiecksverteilte stetige Zufallsgröße X gilt:
$\begin{array}{l}P\left(X<a\right)=0\\ P\left(a\le X\le \frac{a+b}{2}\right)=P\left(\frac{a+b}{2}\le X\le b\right)=\frac{1}{2}\\ P\left(X>b\right)=0\end{array}$

Für die zugehörige Verteilungsfunktion F dieser Zufallsgröße erhält man:
$F\left(x\right)=P\left(X\le x\right)={\displaystyle \underset{-\infty }{\overset{x}{\int }}f\left(t\right)dt=\{\begin{array}{cc}0& fürx<a\\ 2\cdot {\left(\frac{x-a}{b-a}\right)}^2& füra\le x\le \frac{a+b}{2}\\ 1-2\cdot {\left(\frac{b-x}{b-a}\right)}^2& für\frac{a+b}{2}\le x\le b\\ 1& fürx>b\end{array}}$

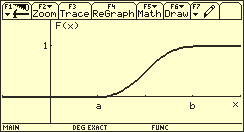
Die beiden wichtigsten Kenngrößen von X, der Erwartungswert und die Streuung, nehmen folgende Werte an:
$EX=\frac{a+b}{2};D^{2}X=\frac{{\left(b-a\right)}^2}{24}$

• Beispiel: Mit einem LAPLACE-Würfel (kurz L-Würfel) werde zweimal gewürfelt und es wird die Summe der geworfenen Augenzahlen gebildet. Die Augensumme ist eine diskrete Zufallsgröße Y mit den elf ganzzahligen Werten 2 bis 12.
  Welche Wahrscheinlichkeitsverteilung P mit $P\left(Y=i\right)=p_i$ besitzt diese Zufallsgröße?

Die folgende Tabelle gibt die Wahrscheinlichkeitsverteilung wieder.

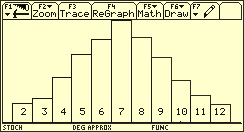
Die Zufallsgröße Y besitzt als Wahrscheinlichkeitsverteilung eine diskrete Dreieckverteilung. Dieses theoretisch gewonnene Ergebnis kann experimentell und interaktiv bestätigt werden, indem man das zweimalige Würfeln mit einem L-Würfel simuliert und 1000 derartige Simulationen als Histogramm darstellen lässt.

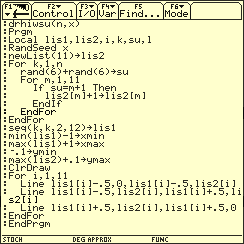
Dieses Ergebnis lässt sich folgendermaßen verallgemeinern:

• Es seien $X_{1}und{X}_2$ zwei unabhängige und über dem Intervall $\left[a;b\right]$ gleichverteilte stetige Zufallsgrößen mit der gleichen Dichtefunktion
  $f:x\mapsto \{\begin{array}{c}\frac{1}{b-a}füra\le x\le b\\ 0sonst\end{array}$
  Dann ist die Zufallsgröße $Y=X_1+X_2$ stetig dreiecksverteilt.