Der Zentrale Grenzwertsatz
Ausgehend von der Erfahrung, dass viele Alltagsphänomene, die sich aus unabhängig voneinander wirkenden kleinen Komponenten zusammensetzen, annähernd normalverteilt sind, richtete sich das Augenmerk mehrerer Mathematikergenerationen vor allem auf die Frage, welche Bedingungen man dafür zu fordern hat.
Auch der Zufall ist nicht unergründlich, er hat seine Regelmäßigkeit. (NOVALIS)
Betrachtet man reale zufällige Prozesse etwas genauer, so wird man feststellen, dass sie nicht selten durch die Überlagerung einer Vielzahl unabhängig voneinander wirkender kleiner Effekte zustande kommen, die selbst zufälligen Charakter tragen. Das trifft z.B. auf natürliche Wachstumsprozesse, auf Messvorgänge oder auf die Einhaltung von Produktionstoleranzen zu.
Mathematisch kann dieser Sachverhalt durch die Summe unabhängiger Zufallsgrößen beschrieben werden. Es stellt sich die Frage, ob die Verteilung der Zufallsgröße , insbesondere für große n, besondere Eigenschaften und Merkmale besitzt.
Wir betrachten dazu das folgende Beispiel:
Beispiel: Gegeben seien die vier diskreten Zufallsgrößen
Die Zufallsgröße nimmt die Werte an.
-
Script zum Berechnen der Verteilunsgmatrix und zum Zeichnen des Histogramms
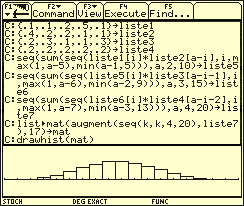
Die Verteilungsmatrix von X kann man mittels eines (vierstufigen, 625-pfadigen und damit recht umfangreichen) Baumdiagramms oder aber mittels Computer berechnen und mit Hilfe eines Diagramms veranschaulichen.
![]()
Das Ergebnis legt die Vermutung nahe, dass bei der Addition unabhängiger Zufallsgrößen für große n eine Normalverteilung entstehen könnte. Der Grenzwertsatz von MOIVRE-LAPLACE stützt diese Annahme für einen Spezialfall, und zwar für den Fall, dass alle die gleiche Verteilung der Gestalt
besitzen.
PIERRE SIMON DE LAPLACE (1749 bis 1827) war überzeugt, dass jede beliebige Zufallsgröße, die man in einzelne Summanden zerlegen kann, einer Normalverteilung folgt, auch wenn man nichts über die Verteilung der einzelnen Summanden weiß. Er konnte dies allerdings nicht beweisen. LAPLACE vermutete es nur intuitiv.
Angesichts der Aussage des Grenzwertsatzes von MOIVRE-LAPLACE und der Erfahrung, dass viele Alltagsphänomene, die sich aus unabhängig voneinander wirkenden kleinen Komponenten zusammensetzen, annähernd normalverteilt sind, richtete sich das Augenmerk mehrerer Mathematikergenerationen vor allem auf die Frage, welche Bedingungen man an die Summanden einer Summe von Zufallsgrößen stellen muss, damit die Summe
für große n annähernd normalverteilt ist.
Es gelang in der Folgezeit, diese Aussage für verschiedene Annahmen über die Summanden zu beweisen. Deshalb existieren auch verschiedene Fassungen des sogenannten Zentralen Grenzwertsatzes. Die heute wohl bekannteste und verbreitetste Fassung geht auf JARL WALDEMAR LINDEBERG (1876 bis 1932) und PAUL PIERRE LÉVY (1886 bis 1971) zurück. Sie besagt Folgendes:
- Es seien unabhängige Zufallsgrößen mit derselben Verteilung, wobei und endlich sind. Setzt man und , dann gilt:
Die Verteilung einer Summe von unabhängigen Zufallsgrößen mit verschiedenen Verteilungen braucht nicht gegen eine Normalverteilung zu konvergieren.
Durch die Untersuchungen zahlreicher Mathematiker konnten aber hinreichende und notwendige Bedingungen bestimmt werden, unter denen der Zentrale Grenzwertsatz gilt, auch wenn die Summanden verschiedene Verteilungen besitzen. Da diese Bedingungen, die hier nicht angegeben werden können, sehr allgemein sind, sind für eine ziemlich umfangreiche Klasse von Folgen unabhängiger Zufallsgrößen die Summen X asymptotisch normalverteilt. Es konnte sogar nachgewiesen werden, dass auch die Verteilung einer Summe schwach abhängiger Zufallsgrößen asymptotisch normalverteilt ist.
Der Zentrale Grenzwertsatz liefert also in seinen unterschiedlichen Fassungen eine theoretische Erklärung dafür, warum so viele verschiedenartige Phänomene des Alltagslebens als annähernd normalverteilt betrachtet werden können und warum die grafische Darstellung relativer Häufigkeiten näherungsweise so oft eine gaußsche Glockenkurve ergibt.

