Normalverteilung (Gauß-Verteilung)
Auf der Suche nach „dem durchschnittlichen, dem normalen Menschen“ (l' homme moyen) ließ der auf vielen Gebieten tätige belgische Wissenschaftler LAMBERT ADOLPHE JACQUES QUÉTELET (1796 bis 1874) in den 30er Jahren des 19. Jahrhunderts biometrische Messungen in großem Umfang durchführen. In vielen Fällen wurde dabei seine Vorstellung bestätigt, dass die Häufigkeitsverteilung der gemessenen Werte (etwa zum Brustumfang) einer symmetrischen Glockenkurve entspricht. Das mag wohl auch ein wichtiger Grund dafür gewesen sein, dieser gleichsam als naturgemäß angesehenen Verteilung den Namen Normalverteilung zu geben, wobei diese Bezeichnung auch zu allerlei Fehldeutungen führte – vor allem dann, wenn alles nicht Normalverteilte als anormal eingestuft wurde.
Das Geburtsdatum der Normalverteilung lag aber fast 100 Jahre früher, als ABRAHAM DE MOIVRE (1667 bis 1754) im Jahre 1733 in einer kleinen Abhandlung die Normalverteilung als Grenzverteilung der Binomialverteilung herleitete.
Die große Anziehungskraft, die von dieser Verteilung auf viele Gelehrte ausging, resultierte hauptsächlich aus den mathematischen Arbeiten von PIERRE SIMON DE LAPLACE (1749 bis 1827) und CARL FRIEDRICH GAUSS (1777 bis 1855), die diese im Zusammenhang mit einer Theorie der Beobachtungsfehler Anfang des 19. Jahrhunderts veröffentlicht hatten. Daran anschließend spricht man auch von der gaußschen Glockenkurve.
Die Normalverteilung, für die im Folgenden eine Definition angegeben wird, zählt auch heute noch zu den bekanntesten und am häufigsten verwendeten Verteilungen.
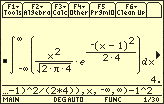
- Definition: Eine stetige Zufallsgröße X mit der Dichtefunktion
heißt normalverteilt mit den Parametern und .
Anmerkung: Man nennt dann die Zufallsgröße X auch oder kurz . Als Schreibweise verwendet man vielfach .
Für die Verteilungsfunktion F einer normalverteilten Zufallsgröße ergibt sich damit:
Der Graph der Dichtefunktion f einer normalverteilten Zufallsgröße ist eine Glockenkurve.
![]()
Führt man (wie in der Analysis) eine Kurvendiskussion durch, so ergibt sich weiterhin:
Der Graph der Dichtefunktion f hat als einzigen Extrempunkt den Hochpunkt (lokalen Maximumpunkt)
,
die Wendepunkte
und die Symmetrieachse mit der Gleichung .
Indem man interaktiv die Werte für und verändert, kann man erkennen, dass sich
- der Graph von f längs der x-Achse verschiebt, falls sich ändert,
- der Graph von f in y-Richtung streckt bzw. staucht, falls sich ändert (je kleiner ist, umso stärker konzentriert sich der Graph von f um den Wert ).
-
Graphen der Dichtefunktionen f (für spezielle Werte)
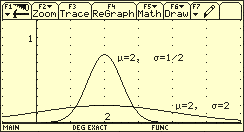
Den Inhalt der Fläche unterhalb des Graphen von f über dem Intervall interpretiert man in der Stochastik (d.h. wenn f als Dichtefunktion einer normalverteilten Zufallsgröße aufgefasst wird) als die Wahrscheinlichkeit .
![]()
Jede Zufallsgröße X mit der Dichtefunktion f besitzt den Erwartungswert .
Dies kann man sich zum einen durch eine Plausibilitätsbetrachtung klarmachen: Der Graph der Dichtefunktion f von verläuft axialsymmetrisch zur Geraden mit der Gleichung .
Folglich kann als Schwerpunkt der Wahrscheinlichkeitsverteilung und somit als Erwartungswert von X betrachtet werden.
Zum anderen lässt sich ferner unter Verwendung von
mit Mitteln der Analysis beweisen, dass gilt:
Schließlich gibt es auch die Möglichkeit, das zur Bestimmung von EX zu berechnende Integral für verschiedene Werte von und interaktiv auszurechnen und zu prüfen, ob sich ergibt.
-
Erwartungswert der Normalverteilung (für spezielle Werte)

Jede Zufallsgröße besitzt die Streuung (bzw. Varianz) .
Auch dies kann man sich durch eine Plausibilitätsbetrachtung verdeutlichen. Der Parameter charakterisiert die Wendestellen des Graphen ihrer Dichtefunktion f.
Je größer ist, desto breiter ist der glockenförmige Graph von f und desto größer müsste demzufolge die Streuung von X sein.
Interaktiv kann man das zur Bestimmung von zu berechnende Integral für verschiedene Werte von und ausrechnen und prüfen, ob sich ergibt.
Die Normalverteilung besitzt eine große praktische Bedeutung, was vor allem aus folgenden Eigenschaften resultiert:
- Mithilfe der Normalverteilung ist es möglich, die Werte der Binomialverteilung näherungsweise zu berechnen.
- Ein zufälliger Vorgang, der durch Überlagerung sehr vieler, kleiner, unabhängiger zufälliger Effekte entsteht, kann näherungsweise durch eine Normalverteilung beschrieben werden. Der zentrale Grenzwertsatz liefert dafür die theoretische Begründung.
- Kann man bei einem zufälligen Vorgang aus inhaltlichen Erwägungen davon ausgehen, dass er sich durch eine Normalverteilung modellieren lässt, so reicht es aus, den Erwartungswert und die Streuung zu bestimmen, denn diese beiden Kennzahlen konstituieren eine Normalverteilung vollständig.
Ist X eine normalverteilte Zufallsgröße mit den Parametern und , dann ist die standardisierte Zufallsgröße ebenfalls normalverteilt, und zwar .
Man bezeichnet diese als standardnormalverteilt und den Graphen ihrer Dichtefunktion als gaußsche Glockenkurve. Wahrscheinlichkeiten für beliebige normalverteilte Zufallsgrößen können demzufolge auf Wahrscheinlichkeiten einer einzigen, speziellen Normalverteilung zurückgeführt werden. Das vereinfacht viele praktische Berechnungen erheblich.
Suche nach passenden Schlagwörtern
- Berechnung
- Glockenkurve
- Standardnormalverteilung
- Mathcad
- gaußsche Glockenkurve
- Schwerpunkt
- normalverteilt
- Verteilungsfunktion
- Quételet
- zentraler Grenzwertsatz
- interaktives Rechenbeispiel
- Zufallsgrößen
- Dichtefunktion
- Wahrscheinlichkeitsverteilung
- Biometrie
- Gauss
- standardnormalverteilt
- Varianz
- Moivre
- Erwartungswert
- Gauß
- Approximation
- Binomialverteilung
- Streuung
- Animation