Gebrochenrationale Funktionen

Bei einer ganzrationalen Funktion ist der Funktionsterm ein Polynom.
Bildet man den Quotienten zweier Polynome, so führt das in der Regel zu einer neuen Funktion. Ist z.B. $\text{p}\left(\text{x}\right)=x^3+2x$ und $g\left(x\right)=3x^2-5$, dann ergibt sich die Funktion $\text{f}\left(\text{x}\right)=\frac{{\text{x}}^{\text{3}}+\text{2x}}{{\text{3x}}^{\text{2}}-\text{5}}$.
Man legt fest:

• Eine Funktion f, deren Funktionsterm ein Quotient zweier Polynome $p\left(x\right)$ und $q\left(x\right)$ ist, heißt gebrochenrationale Funktion.
  Gebrochenrationale Funktionen haben die folgende Form:
  $\begin{array}{l}\text{f}\left(\text{x}\right)=\frac{\text{p}\left(\text{x}\right)}{\text{q}\left(\text{x}\right)}=\frac{{\text{a}}_{\text{n}}{\text{x}}^{\text{n}}+{\text{a}}_{\text{n}-\text{1}}{\text{x}}^{\text{n}-\text{1}}+\mathrm{...}+{\text{a}}_{\text{1}}\text{x}+{\text{a}}_{\text{0}}}{{\text{b}}_{\text{m}}{\text{x}}^{\text{m}}+{\text{b}}_{\text{m}-\text{1}}{\text{x}}^{\text{m}-\text{1}}+\mathrm{...}+{\text{b}}_{\text{1}}\text{x}+{\text{b}}_{\text{0}}}\\ (a_i,b_i\in ℝ;a_n\ne 0;b_m\ne 0)\end{array}$

Beispiele für gebrochenrationale Funktionen sind etwa:

• Beispiel 1: ${\text{f}}_{\text{1}}\left(\text{x}\right)=\frac{{\text{2x}}^{\text{2}}+\text{5x}-\text{3}}{{\text{3x}}^{\text{3}}-\text{2x}+\text{7}}$
• Beispiel 2: ${\text{f}}_{\text{2}}\left(\text{x}\right)=\frac{{\text{x}}^{\text{2}}+\text{1}}{{\text{x}}^{\text{2}}-\text{1}}$
• Beispiel 3: ${\text{f}}_{\text{3}}\left(\text{x}\right)=\frac{{\text{x}}^{\text{2}}-\text{4x}+\text{3}}{\text{x}-\text{2}}$

Ganzrationale Funktionen werden in der Regel nach dem Funktionsgrad eingeteilt. Bei gebrochenrationalen Funktionen ist eine solche Einteilung nicht üblich. Bei dieser Klasse von Funktionen vergleicht man den Grad n der Zählerfunktion mit dem Grad m der Nennerfunktion und trifft folgende Unterscheidung:

1. $n<m$
   f ist eine echt gebrochene rationale Funktion (siehe Beispiel 1)
2. $n\ge m$
   f ist eine unecht gebrochene rationale Funktion (siehe Beispiele 2 und 3)

Bei einer unecht gebrochenen rationalen Funktion kann man den Funktionsterm durch Polynomdivision in einen ganzrationalen Term und einen echt gebrochenen rationalen Term zerlegen. Für die Beispiele 2 und 3 erhält man:
$f_2\left(x\right)=1+\frac{2}{x^2-1}bzw.f_3\left(x\right)=x-2-\frac{1}{x-2}$

Jede gebrochenrationale Funktion ist in ihrem gesamten Definitionsbereich stetig. Während eine ganzrationale Funktion für alle $x\in ℝ$ definiert ist, gehören bei einer gebrochenrationalen Funktion nur die reellen Zahlen zum Definitionsbereich, für die die Nennerfunktion $q\left(x\right)$ verschieden von null ist. Die Stellen x mit $q\left(x\right)=0$ heißen Definitionslücken.

Wir betrachten im Folgenden ein Beispiel ausführlicher.

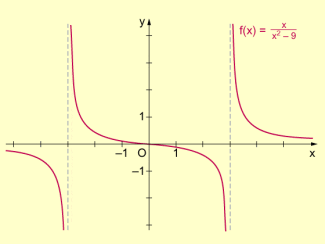
• Beispiel 4: Gegeben sei eine gebrochenrationale Funktion f mit $f\left(\text{x}\right)=\frac{\text{x}}{{\text{x}}^{\text{2}}-\text{9}}$.
  Man bestimme den Definitionsbereich von f und skizziere den Graph.

Da die Nennerfunktion $q\left(\text{x}\right)={\text{x}}^{\text{2}}-\text{9}$ für $x_1=3$ und $x_2=-3$ gleich null ist, gilt für den Definitionsbereich $D_f=ℝ\backslash \left\{-3;3\right\}$. Zwei Definitionslücken zerlegen also den Definitionsbereich (und damit auch den Graphen der Funktion) in drei nicht zusammenhängende Teile. Weitere Anhaltspunkte zum Skizzieren des Graphen, kann eine Wertetabelle liefern.

Die einfachsten Grundtypen gebrochenrationaler Funktionen sind die Funktionen $f\left(x\right)=\frac{1}{x}$ und $g\left(x\right)=\frac{1}{x^2}$.

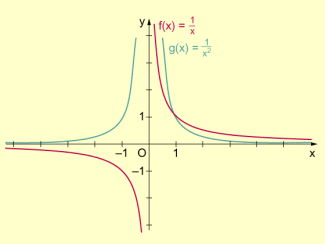
Viele gebrochenrationale Funktionen lassen sich auf diese Grundtypen zurückführen.

• Beispiel 5: Als Beispiel dafür betrachten wir die Funktion h mit $h\left(x\right)=-\frac{2}{x+1}$.

Deren Graph entsteht aus dem Graphen von f, indem man diesen um $-1$ in Richtung der x-Achse verschiebt, anschließend an der x-Achse spiegelt und mit dem Streckungsfaktor $k=2$ in Richtung der x-Achse streckt.