Grafische Darstellung von Daten

Stängel-Blatt-Diagramme

Bei einem Stängel-Blatt-Diagramm erfolgt auf der Grundlage einer Klassenbildung eine Aufspaltung der Daten in einen „Stamm“ und ein „Blatt“ (einseitiges Stängel-Blatt-Diagramm) oder zwei „Blätter" (zweiseitiges Stängel-Blatt-Diagramm).

Dabei werden auf dem „Stamm“ (in der Regel vertikal) die ersten (für eine Gruppe von folgenden Daten übereinstimmenden) Ziffern aufgeschrieben und auf den sich nach rechts oder/und links anschließenden „Blättern“ die folgenden Ziffern. Es handelt sich hierbei um ein „halbgrafisches“ Verfahren, da die Daten (also Zahlen) selbst Aufnahme in die grafische Darstellung finden und durch ihre Anordnung eine Veranschaulichung erfolgt, jedoch keine Umsetzung der Daten in Strecken, Flächen, Kurvenzüge o.Ä. vorgenommen wird.

Stängel-Blatt-Diagramme wurden 1977 von dem amerikanischen Statistiker JOHN TUKEY (1915 bis 2000), dem Begründer der sogenannten explorativen Datenanalyse, für die visuelle Darstellung von Daten vorgeschlagen.

Beispiel 1: Bei einer Gruppe von 50 Mädchen und 50 Jungen unterschiedlichen Alters wurden in ungeordneter Reihenfolge die Körpergrößen (auf Zentimeter genau) gemessen. Die Daten lagen in einem Bereich von etwa 130 cm bis über 200 cm.

Auf dem „Stamm“ tragen wir in diesem Falle die Zahlen 13 bis 20 (also die „Zehner“) und auf den Blättern die jeweils dritte Ziffer (also die „Einer“) ein, und zwar nach links die Mädchengrößen und nach rechts die Jungengrößen.

Das kleinste Mädchen hätte also eine Größe von 139 cm, die Größen der vier kleinsten Jungen betrugen (in der Reihenfolge der Messung) 148 cm, 149 cm, 147 cm bzw.149 cm.

Ist der Datenbereich vergleichsweise groß und ist man nicht an der Reihenfolge interessiert, in welcher die Daten erhoben wurden, so kann die Anfertigung eines Stängel-Blatt-Diagramms bereits während der Datenermittlung erfolgen.

Stabdiagramme

Stabdiagramme (auch Streckendiagramme) werden zur grafischen Veranschaulichung von absoluten oder relativen Häufigkeiten qualitativer oder diskreter quantitativer Merkmale verwendet.

Auf einer der beiden hierzu verwendeten Achsen (meist der horizontalen) trägt man dabei die Ausprägungen des betrachteten Merkmals, in Richtung der zweiten Achse die Häufigkeiten deren Auftretens ab. Die Stab- oder Streckenlänge gibt also die Häufigkeit der jeweiligen Merkmalsausprägung an.

Mitunter nutzt man anstelle von Strecken aus optischen Gründen auch Rechtecke gleicher Breite, was zu Balkendiagrammen führt.

Beispiel 2: Aus den Wahlergebnissen die einzelnen Parteien ergibt sich die Sitzverteilung im Parlament. Die aktuelle Verteilung der insgesamt 200 Sitze möge folgendes Aussehen haben:

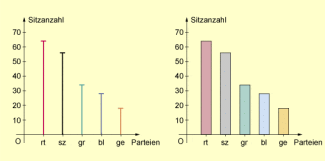
In der folgenden Abbildung ist das zugehörige Stab- bzw. Balkendiagramm dargestellt.

Blockdiagramme

Zur grafischen Veranschaulichung von absoluten oder relativen Häufigkeiten qualitativer oder diskreter quantitativer Merkmale werden auch Blockdiagramme (manchmal Streifendiagramme genannt) verwendet.

Die Gesamtfläche entspricht dabei der Gesamtanzahl (bzw. $100\%$) der erfassten Merkmalsausprägungen ihrer jeweiligen Vielfachheit. Der Flächeninhalt eines Teilrechtecks kennzeichnet die (absolute oder relative) Häufigkeit der dargestellten Merkmalsausprägung (wobei hier die Teilrechtecke immer dieselbe „Höhe“ haben).

Auf den im obigen 2. Beispiel beschriebenen Sachverhalt bezogen erhält man die folgende Darstellung:

Kreisdiagramme

Für die grafische Veranschaulichung der Häufigkeitsverteilung bei qualitativen oder diskreten quantitativen Merkmalen werden auch Kreisdiagramme genutzt.

Der absoluten (oder relativen) Häufigkeit der jeweiligen Merkmalsausprägung entspricht hier der Flächeninhalt des zugehörigen Kreissektors. Dabei ist für die Merkmalsausprägung $a_i\left(i=1;2;\mathrm{...};m\right)$ ein Sektor mit dem Winkel ${\alpha }_i=360°\cdot h_n\left(\left\{a_i\right\}\right)$ zu wählen, wie die folgende Abbildung zeigt.

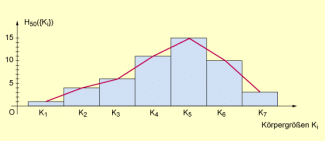
Histogramme

Für die Veranschaulichung von in Klassen eingeteilten Ausprägungen quantitativer Merkmale werden Histogramme ( Säulendiagramme) verwendet.

Hierzu markiert man auf der horizontalen Achse die Klassen $K_i$ von Merkmalsausprägungen und trägt die Klassenmitten $x_i$ ein. Über jeder Klasse wird dann ein Rechteck (eine Säule) gezeichnet, das (die) bei gleicher Breite 1 aller Klassenintervalle die Höhe $H_n\left(\left\{K_i\right\}\right)bzw.h_n\left(\left\{K_i\right\}\right)$ besitzt und jeweils unmittelbar an das Nachbarrechteck anschließt.

Werden für die einzelnen Klassen unterschiedliche Breiten $B\left(K_i\right)$ gewählt, so ist als Höhe des Rechtecks der Wert
$\frac{H_n\left(\left\{K_i\right\}\right)}{B\left(K_i\right)}bzw.\frac{h{}_n\left(\left\{K_i\right\}\right)}{B\left(K_i\right)}$
zu wählen. In diesem Fall entspricht nicht die Höhe, sondern der Flächeninhalt des Rechtecks der jeweiligen absoluten bzw. relativen Häufigkeit.

Wir verwenden den im 1. Beispiel dargestellten Sachverhalt und wählen als einheitliche Klassenbreite jeweils $B=10.$ Dann erhält man (auf das „Mädchen-Blatt“ bezogen) folgende absolute Häufigkeiten $H_{50}\left(\left\{K_i\right\}\right)$:

Die Werte $H_{50}\left(\left\{K_i\right\}\right)$ entsprechen jeweils den Rechteckhöhen in der folgenden Abbildung:

Würde man für die Intervalle [130; 140[, [140; 150[, [150; 160[ und [190; 200[ wegen der geringen „Besetzung“ beispielsweise als Klassenbreite nur die Hälfte der Klassenbreiten der anderen Intervalle wählen, so wären als Rechteckhöhen für die sieben Intervalle die Werte 2, 8, 12, 11, 15, 10, 6 zu verwenden.

Eine solche Darstellung erschwert allerdings den Überblick und kann bei flüchtiger Betrachtung sogar zu Fehleinschätzungen führen.

Polygonzug

Vom Histogramm kann man zu einem Polygonzug übergehen, indem man die Mittelpunkte der oberen Rechteckseiten durch Strecken verbindet.

Dies ist offenbar nur dann sinnvoll, wenn sich dem Abszissenwert jedes Punktes des Polygonzuges auch eine Merkmalsausprägung zuordnen lässt, wenn es sich also um ein stetiges quantitatives Merkmal handelt.