Interessante Kurven

Traktrix (Schleppkurve)

Ein Punkt P am Ende eines nicht dehnbaren Seiles der Länge l beschreibt eine Traktrix oder Schleppkurve (Hundekurve), wenn das Seil vom Punkt S, der sich auf der x-Achse bewegt, gezogen wird. Die Länge des Tangentenstückes von der Kurve zur x-Achse ist also konstant. Für diese Kurve gilt:
$\begin{array}{c}x=l\cdot ar\cosh \left(\frac{l}{y}\right)+\sqrt{l^2-y^2}\\ =l\cdot \ln \left(\frac{l-\sqrt{l^2-y^2}}{y}\right)+\sqrt{l^2-y^2 } \end{array}$

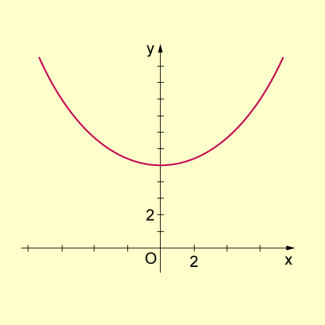
Kettenlinie

Die Kettenlinie entsteht bei der Aufhängung eines schweren biegsamen Fadens (dünne Kette) zwischen zwei Punkten. Es gilt:
$y=f\left(x\right)=a\cdot \frac{e^{\frac{x}{a}}+e^{-\frac{x}{a}}}{2}$

In der folgenden Abbildung ist die Kurve für $a=5$ dargestellt.

Anmerkung: Eine rationale Näherung in der Nähe des Scheitelpunktes erhält man mit:
$y=g\left(x\right)=\frac{x^2}{2a}+a$

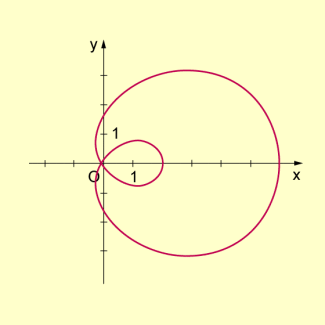
Pascalsche Schnecke

Die pascalsche Schnecke ist die Konchoide des Kreises. In Parameterform gilt:
$\begin{array}{l}x=a\cdot {\cos }^2\varphi +l\cdot \cos \varphi \\ y=a\cdot \sin \varphi \cos \varphi +l\cdot \sin \varphi \end{array}$

In der folgenden Abbildung ist die Kurve für $a=4$ und $l=2$ dargestellt.
Die Gleichung in Polarkoordinaten lautet:
$r\left(\varphi \right)=a\cdot \cos \varphi +l\cdot \sin \varphi$

Die folgenden wichtigen Kurven sind vorwiegend mit Mitteln der Differenzialgeometrie zu erhalten (dabei treten bei der Lösung der Fragestellung Differenzialgleichungen auf, die hier nicht diskutiert werden).

• Die Evolute ist der geometrische Ort aller Krümmungsmittelpunkte einer ebenen Kurve.

Die Evolute der Parabel $y=x^2$ erhält man in folgender Form:
$y=\frac{1}{2}+3\cdot {\left(\frac{x}{4}\right)}^{\frac{2}{3}}$
(bzw. in Parameterdarstellung)
$\begin{array}{c}x\left(t\right)=-4t^3\\ y\left(t\right)=\frac{1+6t^2}{2}\end{array}$

• Wird ein Faden um eine Kurve gelegt und dann straff abgewickelt, so beschreibt das Fadenende eine Evolvente (Abwickelkurve). Anwendung finden die Evolventen z.B. in der Zahnradformung.

Für den Kreis lautet die Evolvente in Parameterdarstellung folgendermaßen:
$\begin{array}{c}x\left(\varphi \right)=r\cdot \left(\cos \varphi +\varphi \cdot \sin \varphi \right)\\ y\left(\varphi \right)=r\cdot \left(\sin \varphi -\varphi \cdot \cos \varphi \right)\end{array}\left(rRadius;\varphi Wälzwinkel\right)$

Die Einhüllende (Enveloppe) entsteht, wenn eine Kurvenschar betrachtet wird.
Die Geradenschar beispielsweise, bei der beim Schnitt mit den Koordinatenachsen sich jeweils eine Strecke der konstanten Länge l ergibt, wird durch die Astroide mit folgender Gleichung eingehüllt:
$x^{\frac{2}{3}}+y^{\frac{2}{3}}=l^{\frac{2}{3}}$