Kugel und Gerade
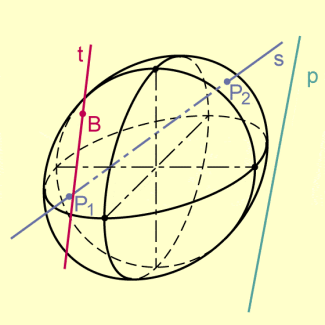
Für die Lage einer Kugel bezüglich einer Geraden gibt es die folgenden Möglichkeiten:
- Kugel und Gerade haben keinen Punkt gemeinsam (Fall 1);
- Kugel und Gerade haben genau einen Punkt gemeinsam (Fall 2);
- Kugel und Gerade haben genau zwei Punkte gemeinsam (Fall 3)
Im Fall 1 nennt man die Gerade eine Passante, im Fall 2 eine Tangente und im Fall 3 eine Sekante.
-
Lagemöglichkeiten von Gerade und Kugel
Will man die Lage einer in Parameterdarstellung gegebenen Geraden g bezüglich einer Kugel k untersuchen, so setzt man für x, y, z in der Kugelgleichung die entsprechenden Koordinaten eines beliebigen Punktes der Geraden ein.
Erhält man beim Lösen dieser Gleichung für den Parameter der Geraden genau zwei Werte, so ist die Gerade eine Sekante. Erhält man genau einen Wert, so handelt es sich um eine Tangente. Ist die Gleichung nicht lösbar, so passiert die Gerade die Kugel.
Durch Einsetzen des Wertes (bzw. der Werte) für den Parameter in die Geradengleichung ergeben sich die Koordinaten des gemeinsamen Punktes (bzw. der gemeinsamen Punkte) von Gerade und Kugel.
- Beispiel 1:
Die Kugelgleichung lautet .
Einsetzen der Koordinaten von ergibt dann:
Also ist g eine Sekante, welche die Kugel in den Punkten schneidet.
- Beispiel 2:
Einsetzen von P in die Kreisgleichung ergibt:
Also ist die Gerade g eine Tangente mit dem Berührungspunkt .
- Beispiel 3:
Durch Einsetzen von P in die Kreisgleichung erhält man:
Es existiert keine Lösung, also ist die Gerade g eine Passante.
Alle Geraden, die eine Kugel k in demselben Punkt berühren, also Tangenten mit demselben Berührungspunkt sind, liegen in einer Ebene, der Tangentialebene.
-
Tangentialebene der Kugel
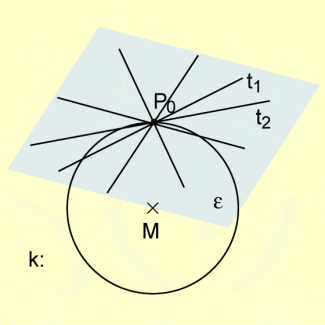
Will man von einem Punkt außerhalb der Kugel eine Tangente an die Kugel legen, so gibt es unendlich viele Geraden, die durch diesen Punkt verlaufen und die Kugel jeweils in genau einem Punkt berühren, also Tangenten an die Kugel sind. Diese Geraden bilden zusammen einen Tangentialkegel.
- Beispiel 4: An die Kugel k mit dem Mittelpunkt und dem Radius sollen vom Punkt aus Tangenten gelegt werden.
Es gibt unendlich viele Tangenten. Zwei davon sind z.B. die folgenden:
Sie berühren die Kugel – wie man rechnerisch nachweisen kann – im Punkt

