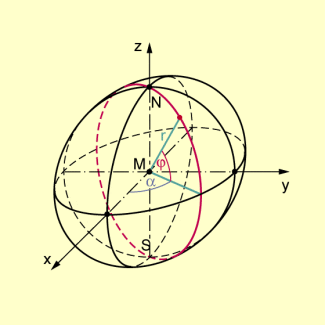Kugelgleichungen
Ausgehend vom Begriff der Kugel lassen sich mithilfe eines kartesischen Koordinatensystems Gleichungen (in vektorieller Form und als Koordinatengleichungen) entwickeln. Eine Kugel kann auch durch eine Parametergleichung beschrieben werden.
Eine Kugel ist die Menge aller der Punkte des Raumes, die von einem gegebenen Punkt M denselben Abstand r haben. Dabei ist M der Mittelpunkt der Kugel mit den Koordinaten , r der Radius und ein beliebiger Punkt der Kugel.
Mithilfe eines kartesischen Koordinatensystems lassen sich analytische Ausdrücke finden, die die Lage dieser Punkte im Raum eindeutig beschreiben.
-
Kugel in Mittelpunktslage
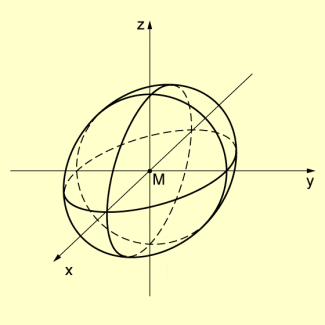
Vektorielle Gleichung und Koordinatengleichung
Befindet sich der Mittelpunkt der Kugel im Koordinatenursprung O, so ist der Betrag des Ortvektors zu einem beliebigen Punkt P der Kugel gleich dem Radius r.
Für diese Mittelpunktslage gilt die folgende vektorielle Gleichung:
Aus dieser Gleichung lässt sich durch Ausführen der skalaren Multiplikation die Koordinatengleichung ermitteln:
- Beispiel 1: Eine Kugel mit wird durch die vektorielle Gleichung bzw. die Koordinatengleichung beschrieben.
-
Kugel in allgemeiner Lage
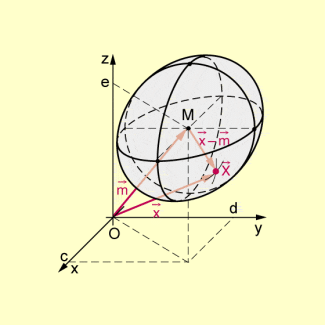
Liegt der Mittelpunkt der Kugel jedoch nicht im Koordinatenursprung, so ist der Betrag des Vektors gleich dem Radius der Kugel.
Wegen gilt für diese allgemeine Lage:
Durch Ausführen der skalaren Multiplikation erhält man aus dieser vektoriellen Gleichung wiederum die entsprechende Koordinatengleichung:
- Beispiel 2: Eine Kugel mit wird durch die folgenden Gleichungen beschrieben:
Jede Kugelgleichung ermöglicht es uns, die Koordinaten des Mittelpunktes und den Radius der Kugel zu ermitteln.
Dies funktioniert selbst dann, wenn die quadratische Gleichung nicht in der Form gegeben ist.
Durch Umformen und quadratische Ergänzung schafft man sich die gewünschte Form der allgemeinen Koordinatengleichung einer Kugel.
- Beispiel 3:
Man formt die gegebene Gleichung um in
und erhält nach Ausführen der quadratischen Ergänzung und Zusammenfassen;
Also wird durch diese Gleichung eine Kugel mit dem Mittelpunkt und dem Radius beschrieben.
Anmerkung: Sollte sich beim Umformen einer solchen Gleichung auf der rechten Seite jedoch eine Zahl kleiner gleich null ergeben, kann es sich nicht um eine Kugelgleichung handeln, denn muss stets größer als null sein.
Parametergleichung
Eine Kugel kann aber auch durch eine Parametergleichung beschrieben werden. Man denke sich vom Mittelpunkt der Kugel einen Strahl ausgehend, der zu einem beliebigen Punkt der Kugel führt. Mithilfe zweier Winkel zwischen dem Strahl und einer zur xy-Ebene parallelen Ebene bzw. dem Strahl und einer zur yz-Ebene parallelen Ebene lassen sich die Koordinaten der Kugelpunkte beschreiben.
-
Zur Parameterdarstellung der Kugel
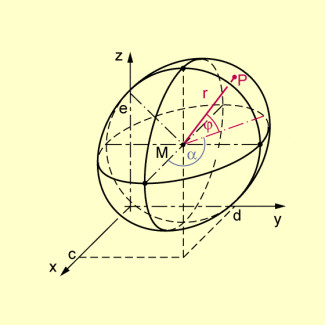
Es gilt:
- Beispiel (Gradnetz der Erde): Die Erde kann näherungsweise als Kugel mit einem Radius angesehen werden.
Punkte auf der Erde werden durch die Angabe der geografischen Breite (Winkel zwischen Strahl und Äquatorebene) und der geografischen Länge (Winkel zwischen Strahl und Nullmeridian) beschrieben.
So hat z.B. die Stadt Schwerin die folgenden Werte:
-
Gradnetz der Erde