Lagebeziehungen zweier Kugeln

Zwei Kugeln im Raum können – abgesehen von dem Fall, dass beide Kugeln identisch sind – verschiedene Positionen zueinander einnehmen.

Kim hat in Deutsch, Mathe, Englisch und 6 weiteren Schulfächern immer eine von Lehrkräften geprüfte Erklärung, Video oder Übung parat.
24/7 auf Learnattack.de und WhatsApp mit Bildupload und Sprachnachrichten verfügbar. Ideal, um bei den Hausaufgaben und beim Lernen von Fremdsprachen zu unterstützen.
Viel günstiger als andere Nachhilfe und schützt deine Daten.

Jetzt 30 Tage risikofrei testen

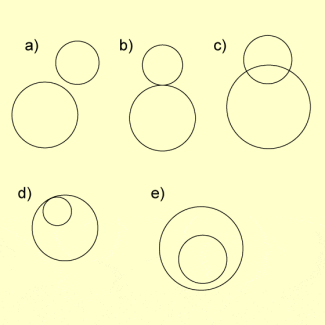
Fall 1: Beide Kugeln haben keinen gemeinsamen Punkt (a und e).
Fall 2: Beide Kugeln haben genau einen gemeinsamen Punkt (b und d).
Fall 3: Beide Kugeln haben unendlich viele Punkte gemeinsam, die zu einem Kreis gehören, dem Schnittkreis der beiden Kugeln (c).

Entscheidend für die Anzahl der gemeinsamen Punkte ist der Abstand d der Mittelpunkte der beiden Kugeln:

Wenn $d = \bar{M_{1} M_{2}} = r_{1} + r_{2}$ ist, dann liegt der Fall 2 vor.
Wenn $d > r_{1} + r_{2}$ bzw. $d < | r_{1} - r_{2} |$ gilt, dann liegt der Fall 1 vor.
Wenn $d < r_{1} + r_{2}$ bzw. $d > | r_{1} - r_{2} |$ gilt, dann liegt der Fall 3 vor.

Daher beginnt man die Untersuchung der Lagebeziehung zweier Kugeln mit dem Vergleich der Streckenlänge von $d = \bar{M_{1} M_{2}}$ mit $r_{1} + r_{2}$ bzw. $| r_{1} - r_{2} |$ .

Berechnen des Berührungspunktes zweier Kugeln

Liegt Fall 2 vor, ermittelt man den gemeinsamen Berührungspunkt , indem man die Gleichung der Geraden g durch $M_{1} u n d M_{2}$ aufstellt und durch Einsetzen in eine der beiden Kugelgleichungen zunächst den Parameterwert und daraus dann die Koordinaten des Berührungspunktes erhält.

Beispiel 1:
$\begin{array}{l} k_{1} : M_{1} (1; 0; 4); r_{1} = 1; {(x - 1)}^{2} + y^{2} + {(z - 4)}^{2} = 1 \\ k_{2} : M_{2} (3; - 1; 6); r_{2} = 2; {(x - 3)}^{2} + {(y + 1)}^{2} + {(z - 6)}^{2} = 4 \end{array}$

Gerade g, auf der beide Mittelpunkte liegen:
$\vec{x} = (\begin{matrix} 1 \\ 0 \\ 4 \end{matrix}) + t \cdot (\begin{matrix} 2 \\ - 1 \\ 2 \end{matrix}); t \in ℝ$
Einsetzen in die Gleichung von $k_{1}$ ergibt:
$\begin{matrix} {(1 + 2 t - 1)}^{2} + {(- t)}^{2} + {(4 + 2 t - 4)}^{2} = 1 \\ 9 t^{2} = 1 \\ t^{2} = \frac{1}{9} \end{matrix}$
Die Lösung $t = - \frac{1}{3}$ scheidet aus, da der Berührungspunkt in diesem Fall nicht zwischen $M_{1} u n d M_{2}$ liegen würde. Damit ergibt sich $t = \frac{1}{3}$ , und die Koordinaten des Berührungspunktes lauten:
$B (\frac{5}{3}; - \frac{1}{3}; \frac{14}{3})$

Berechnen des Schnittkreises zweier Kugeln

Liegt Fall 3 vor, kann man zunächst die gemeinsame Schnittebene aus der Differenz der beiden Kugelgleichungen ermitteln, dann den Mittelpunkt des Schnittkreis es als Durchstoßpunkt der Geraden durch $M_{1} u n d M_{2}$ mit der Schnittebene bestimmen und Radius des Schnittkreises durch Anwenden des Satzes des PYTHAGORAS berechnen.

Bild

Es sei $M'$ der Mittelpunkt des Schnittkreises, d der Abstand der Mittelpunkte $M_{1} u n d M_{2}$ , $d_{1}$ der Abstand des Mittelpunktes $M_{1} v o n M'$ , $d_{2}$ der Abstand des Mittelpunktes $M_{2} v o n M'$ .
Es gelten also folgende Gleichungen:
$d = \bar{M_{1} M_{2}} d_{1} = \bar{M_{1} M'} d_{2} = d - d_{1} = \bar{M_{2} M'}$
Für die Radien ergibt sich:
$\begin{array}{l} r_{1}^{2} = r'^{2} + d_{1}^{2} r_{2}^{2} = r'^{2} + d_{2}^{2} \\ r_{1}^{2} - r_{2}^{2} = d_{1}^{2} - d_{2}^{2} = d_{1}^{2} - d^{2} + 2 d d_{1} - d_{1}^{2} = 2 d d_{1} - d^{2} \end{array}$
Durch Umstellen folgt:
$\begin{array}{l} d_{1} = \frac{r_{1}^{2} - r_{2}^{2} + d^{2}}{2 d} \\ r' = \sqrt{r_{1}^{2} - d_{1}^{2}} \end{array}$

Beispiel 2:
$\begin{array}{l} k_{1} : M_{1} (1; 3; 9); r_{1} = 7 \\ k_{2} : M_{2} (2; - 1; 5); r_{2} = 4 \end{array}$

Die Kreisgleichungen lauten:
$\begin{array}{l} k_{1} : {(x - 1)}^{2} + {(y - 3)}^{2} + {(z - 9)}^{2} = 49 \\ x^{2} - 2 x + 1 + y^{2} - 6 y + 9 + z^{2} - 18 z + 81 = 49 \\ x^{2} + y^{2} + z^{2} - 2 x - 6 y - 18 z = - 42 \\ k_{2} : {(x - 2)}^{2} + {(y + 1)}^{2} + {(z - 5)}^{2} = 16 \\ x^{2} - 4 x + 4 + y^{2} + 2 y + 1 + z^{2} - 10 z + 25 = 16 \\ x^{2} + y^{2} + z^{2} - 4 x + 2 y - 10 z = - 14 \end{array}$
Jeder Punkt $P (x; y; z)$ , der sowohl zu $k_{1}$ als auch zu $k_{2}$ gehört, muss auch die Gleichung erfüllen, die sich als Differenz der zu $k_{1} u n d k_{2}$ gehörenden Gleichungen ergibt. Diese lautet:
$2 x - 8 y - 8 z = - 28$
Schnittebene $ε$ : $x - 4 y - 4 z = - 14$
Die Gerade $g_{M_{1} M_{2}}$ , welche die Mittelpunkte $M_{1} u n d M_{2}$ verbindet, ist durch die folgende Punktrichtungsgleichung gegeben:
$g_{M_{1} M_{2}} : \vec{x} = (\begin{matrix} 1 \\ 3 \\ 9 \end{matrix}) + t \cdot (\begin{matrix} 1 \\ - 4 \\ - 4 \end{matrix}); t \in ℝ$
Durch Einsetzen von $g_{M_{1} M_{2}}$ in die Gleichung der Ebene $ε$ erhält man:
$\begin{matrix} (1 + t) - 4 \cdot (3 - 4 t) - 4 \cdot (9 - 4 t) = - 14 \\ 33 t = 33 \\ t = 1 \end{matrix}$
Mittelpunkt des Schnittkreises: $M' (2; - 1; 5)$
Radius des Schnittkreises $r'$ :
$\begin{array}{l} d = \bar{M_{1} M_{2}} = \sqrt{33} \\ d_{1} = \frac{r_{1}^{2} - r_{2}^{2} + d^{2}}{2 d} = \frac{49 - 16 + 33}{2 \cdot \sqrt{33}} = \frac{66}{2 \cdot \sqrt{3}} = \sqrt{33} \\ r' = \sqrt{r_{1}^{2} - d_{1}^{2}} = \sqrt{49 - 33} = 4 \end{array}$
Damit hat der Schnittkreis beider Kugeln den Mittelpunkt $M' (2; - 1; 5)$ und den Radius $r' = 4$ und liegt in der Ebene $x - 4 y - 4 z = - 14$ .

Falls sich zwei Kugeln $k_{1} u n d k_{2}$ in genau einem Punkt berühren, dann gibt es für beide Kugeln in diesem Berührungspunkt eine gemeinsame Tangentialebene. Diese Tangentialebene kann von besonderem Interesse sein, z.B. beim Billardspiel. Wenn beim Billardspiel zwei Kugeln aneinanderstoßen, wird die angestoßene Kugel senkrecht zur gemeinsamen Tangentialebene beschleunigt.

Beispiel 3:
> $\begin{array}{l} k_{1} : M_{1} (4; 5; 6); r_{1} = 10 \\ k_{2} : M_{2} (1; 1; - 4); r_{2} = 3 \end{array}$

Die Kugelgleichungen lauten:
$\begin{array}{l} k_{1} : {(x - 4)}^{2} + {(y - 5)}^{2} + {(z - 6)}^{2} = 100 \\ x^{2} + y^{2} + z^{2} - 8 x - 10 y - 12 z = 23 \\ k_{2} : {(x - 1)}^{2} + {(y - 1)}^{2} + {(z + 4)}^{2} = 9 \\ x^{2} + y^{2} + z^{2} - 2 x - 2 y + 8 z = - 9 \end{array}$
Gleichung der Schnittebene $ε$ :
$\begin{array}{l} - 6 x - 8 y - 20 z = 32 \\ - 3 x - 4 y - 10 z = 16 \end{array}$
$g_{M_{1} M_{2}} : \vec{x} = (\begin{matrix} 4 \\ 5 \\ 6 \end{matrix}) + t \cdot (\begin{matrix} 3 \\ 4 \\ 10 \end{matrix}); t \in ℝ$
Schnittpunkt von $g_{M_{1} M_{2}} u n d ε$ :
$\begin{matrix} - 3 \cdot (4 + 3 t) - 4 \cdot (5 + 4 t) - 10 \cdot (6 + 10 t) = 16 \\ - 125 t = 108 \\ t = - \frac{108}{125} \end{matrix}$
Mittelpunkt des Schnittkreises: $M' (\frac{176}{125}; \frac{193}{125}; - \frac{66}{25})$
$\begin{array}{l} d = \bar{M_{1} M_{2}} = \sqrt{125} \\ d_{1} = \frac{r_{1}^{2} - r_{2}^{2} + d^{2}}{2 d} = \frac{100 - 9 + 125}{2 \cdot \sqrt{125}} = \frac{108}{\sqrt{125}} \\ r' = \sqrt{r_{1}^{2} - d_{1}^{2}} = \sqrt{100 - \frac{11664}{125}} = \sqrt{\frac{836}{125}} = \frac{2 \cdot \sqrt{1045}}{25} \approx 2,6 \end{array}$

Lernhelfer (Duden Learnattack GmbH): "Lagebeziehungen zweier Kugeln." In: Lernhelfer (Duden Learnattack GmbH). URL: http://www.lernhelfer.de/index.php/schuelerlexikon/mathematik-abitur/artikel/lagebeziehungen-zweier-kugeln (Abgerufen: 20. May 2025, 18:14 UTC)

Suche nach passenden Schlagwörtern

Jetzt durchstarten

Entspannt durch die Schule mit KI-Tutor Kim und Duden Learnattack.

Kim hat in Deutsch, Mathe, Englisch und 6 weiteren Schulfächern immer eine von Lehrkräften geprüfte Erklärung, Video oder Übung parat.
24/7 auf Learnattack.de und WhatsApp mit Bildupload und Sprachnachrichten verfügbar. Ideal, um bei den Hausaufgaben und beim Lernen von Fremdsprachen zu unterstützen.
Viel günstiger als andere Nachhilfe und schützt deine Daten.

Lagebeziehungen zweier Kugeln

Schule wird easy mit KI-Tutor Kim und Duden Learnattack

Berechnen des Berührungspunktes zweier Kugeln

Berechnen des Schnittkreises zweier Kugeln

Suche nach passenden Schlagwörtern