Kugel und Ebene
Eine Kugel und eine Ebene können keinen Punkt (Fall 1), genau einen Punkt (Fall 2) oder unendlich viele Punkte, die auf einem Kreis (dem Schnittkreis) liegen (Fall 3), gemeinsam haben.
-
Lagemöglichkeiten von Ebene und Kugel
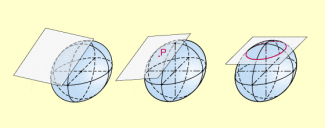
Besitzen Kugel und Ebene genau einen gemeinsamen Punkt (Fall 2), dann heißt die Ebene Tangentialebene.
Um festzustellen, welche der drei Möglichkeiten vorliegt, ermittelt man den Abstand d der Ebene vom Mittelpunkt M der Kugel k:
- Wenn ist, so gibt es keinen gemeinsamen Punkt.
(Fall 1) - Wenn ist, so existiert genau ein gemeinsamer Punkt, ist Tangentialebene.
(Fall 2) - Wenn , so schneidet die Ebene die Kugel k, es gibt unendlich viele gemeinsame Punkte, die einen Schnittkreis bilden.
(Fall 3)
Im Fall 2 (Tangentialebene) lässt sich der Berührungspunkt als Durchstoßpunkt der Geraden g durch den Mittelpunkt M der Kugel k mit Richtung des Normalenvektors der Ebene ermitteln.
Im Fall 3 (es existiert ein gemeinsamer Schnittkreis von Kugel k und Ebene ) können der Mittelpunkt und der Radius des Schnittkreises s berechnet werden.
Den Mittelpunkt erhält man als Durchstoßpunkt der Geraden durch den Mittelpunkt M der Kugel k in Richtung des Normalenvektors der Ebene .
Den Radius des Schnittkreises berechnet man mithilfe des Satzes des PYTHAGORAS:
![]()
- Beispiel 1: Gegeben sind eine Kugel k mit sowie eine Ebene durch ihre Gleichung .
Der Abstand d des Mittelpunktes M der Kugel k von der Ebene beträgt:
Damit ist , Kugel k und Ebene haben also keinen gemeinsamen Punkt.
- Beispiel 2: Gegeben sind eine Kugel k mit sowie eine Ebene durch ihre Gleichung .
Der Abstand d des Kugelmittelpunktes M von der Ebene beträgt:
Somit ist , also existiert genau ein gemeinsamer Punkt , die Ebene ist Tangentialebene an die Kugel k.
Nun werden die Koordinaten des Berührungspunktes ermittelt. Die Gerade g durch den Mittelpunkt M der Kugel in Richtung des Normalenvektors der Ebene wird durch folgende Gleichung beschrieben:
Durch Einsetzen der Koordinaten eines Punktes der Geraden in die Ebenengleichung erhält man den Wert des Parameters t:
Damit ist der gesuchte Berührungspunkt.
- Beispiel 3: Gegeben sind eine Kugel k mit sowie eine Ebene durch ihre Gleichung .
Der Abstand d des Kugelmittelpunktes M von der Ebene beträgt:
Damit ist , die Ebene schneidet also die Kugel k.
Die Koordinaten des Mittelpunktes des Schnittkreises und sein Radius werden ermittelt durch Aufstellen der Gleichung für die Geraden durch M in Richtung des Normalenvektors der Ebene und Einsetzen in die Ebenengleichung:
Man erhält schließlich:

