Monotonie von Funktionen

Steigt der Graph, so wachsen die Funktionswerte, d.h., für $x_1<x_2$ ist auch $f\left(x_1\right)<f\left(x_2\right)$. In diesem Fall heißt die Funktion in dem betrachteten Intervall streng monoton wachsend. Ist das nicht nur in einem bestimmten Intervall, sondern im gesamten Definitionsbereich $D_f$ der Fall, so heißt die Funktion streng monoton wachsend.

Gilt dagegen $f\left(x_1\right)>f\left(x_2\right)$ für $x_1<x_2$, dann spricht man von streng monoton fallend.

Für das Monotonieverhalten einer Funktion gilt:

• Eine Funktion f heißt in einem Intervall I ihres Definitionsbereichs $D_f$ genau dann monoton wachsend, wenn für beliebige $x_1,x_2\in I$ gilt:
  $x_1<x_2\Rightarrow f\left(x_1\right)\le f\left(x_2\right)$
  Gilt sogar $x_1<x_2\Rightarrow f\left(x_1\right)<f\left(x_2\right)$, so heißt f streng monoton wachsend.
• Eine Funktion f heißt in einem Intervall I ihres Definitionsbereichs $D_f$ genau dann monoton fallend, wenn für beliebige $x_1,x_2\in I$ gilt:
  $x_1<x_2\Rightarrow f\left(x_1\right)\ge f\left(x_2\right)$
  Gilt sogar $x_1<x_2\Rightarrow f\left(x_1\right)>f\left(x_2\right)$, so heißt f streng monoton fallend.

Die Untersuchung von Funktionen auf Monotonie ist mithilfe der soeben gegebenen Erklärung oft nicht einfach. Ist die Funktion f aber differenzierbar dann liefert der Zusammenhang zwischen der Monotonie von f und den Tangentensteigungen das nachfolgende Kriterium für strenge Monotonie:
Sei f eine im Intervall I differenzierbare Funktion. Wenn für alle x aus I

1. $f^{\prime }\left(x\right)>0$ gilt, dann ist f in I streng monoton wachsend;
2. $f^{\prime }\left(x\right)<0$ gilt, dann ist f in I streng monoton fallend

Wir betrachten im Folgenden einige Beispiele für Monotonieuntersuchungen.

Beispiel 1: Die Funktion $f\left(x\right)=2^x$ ist mithilfe der Definition auf Monotonie zu untersuchen.

Sind $x_1,x_2\in D_f$ mit $x_1<x_2$, dann ist $x_2=x_1+h$ mit $h>0$.
Für den Funktionswert gilt dann:
$f\left(x_2\right)=2^{x_2}=2^{x_1+h}=2^{x_1}\cdot 2^h$
Für $h>0$ ist $2^h>1$, also ist:
$f\left(x_2\right)=2^{x_1}\cdot 2^h>2^{x_1}=f\left(x_1\right)$
Das heißt, f(x) ist streng monoton wachsend über dem gesamten Definitionsbereich.

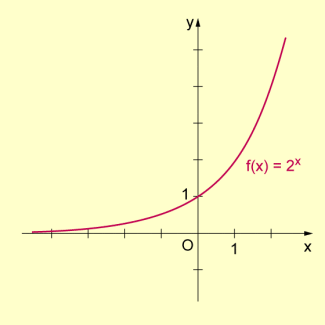
Beispiel 2: Die Funktion $f(x)=\frac{2}{3}{x}^3+x$ ist mithilfe des Monotoniekriteriums auf Monotonie zu untersuchen.

Die 1. Ableitung ist $f^{\prime }(x)=2x^2+1$. Die Ungleichung $2x^2+1>0$ ist für alle $x\in ℝ$ erfüllt, d.h. die Funktion ist im gesamten Definitionsbereich streng monoton wachsend.

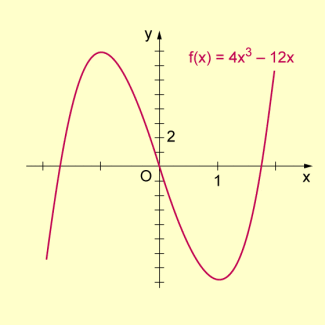
Beispiel 3: Das Montonieverhalten der Funktion $f\left(x\right)=4x^3-12x$ ist zu untersuchen.

Auch hier wendet man zweckmäßigerweise das Monotoniekriterium an.
Man erhält $f^{\prime }\left(x\right)=12x^2-12$.
Die Ungleichung $12x^2-12>0$ bzw. $x^2-1>0$ ist erfüllt für $x<-1$ oder $x>1$. Die Ungleichung $12x^2-12<0$ bzw. $x^2-1<0$ ist erfüllt für $-1<x<1$.
Also ist die Funktion f für $x<-1$ und $x>1$ streng monoton wachsend und für $-1<x<1$ streng monoton fallend.